遷移状態の計算方法の説明(TS、SADDLE)

計算の意味: 反応物から生成物の化学反応が進行する時にエネルギー的に極大点であることを遷移状態といい、その構造を解析する事によりこの化学反応をより詳しく解明する事が出来る。ここでは、計算方法について簡単に説明する。

計算手順

初期構造の作成

遷移状態の構造最適化

遷移状態である事の確認

目的の遷移状態である事の確認(反応物、生成物への変化の確認)

初期構造の作成

「SADDLE」というキーワードを用いる方法と、「反応座標の手法」を用いる方法がある。

「反応座標の手法」の説明

その化学反応を特徴づけるような内部座標を反応座標として選び、入力データの最適化フラグを-1にして、データの最後に何点かの反応座標値を付け加えることにより、各点でのエネルギー値を計算する。その極大点を、遷移状態に近い初期状態として仮定する。

CH₂CH₂ + CH₂CH₃　→　 CH₂CH₂CH₂CH₃ の化学反応の例を以下に示す。

入力データ

 PM3  UHF SYMMETRY 
 CHPTER 10 
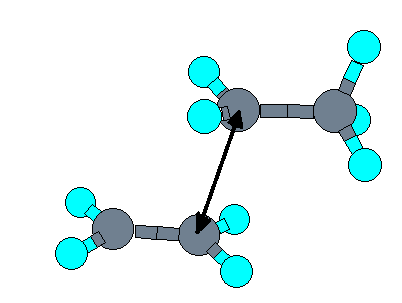
 C2H4 + C2H5 -> C4H9
  C    0.0000  0    0.0000  0    0.0000  0    0   0   0
  C    1.3219  1    0.0000  0    0.0000  0    1   0   0
 XX    1.0000  0  180.0000  0    0.0000  0    1   2   0  ←"XX"はダミー原子
  H    1.0900  1  120.0000  1   90.0000  0    1   2   3     構造の定義のみに使用
  H    1.0900  0  120.0000  0  -90.0000  1    1   2   3
  H    1.0900  1  120.0000  1  -90.0000  1    2   1   3
  H    1.0900  0  120.0000  0   90.0000  0    2   1   3
  C   50.0000 -1  100.0000  1    0.0000  0    2   1   3  ←"-1" のあるところが
  C    1.4560  1  100.0000  1  180.0000  0    8   2   1         反応座標である。
  H    1.1000  1  110.0000  1  180.0000  0    9   8   2
  H    1.1000  1  110.0000  1   60.0000  1    9   8   2
  H    1.1000  0  110.0000  0  -60.0000  0    9   8   2
  H    1.0800  1  120.0000  1  -90.0000  1    8   9  10
  H    1.0800  0  120.0000  0   90.0000  0    8   9  10
  0    0.0000  0    0.0000  0    0.0000  0    0   0   0  ←構造定義終了
  4   1    5  ←  対称の定義
  4   2    5          ・
  6   1    7          ・
  6   2    7  ←  対称の定義
  6  14    7          ・
 11   1   12          ・
 11   2   12          ・
 11  14   12  ←  対称の定義
 13   1   14          ・
 13   2   14          ・
 13  14   14  ←  対称の定義
                                       ← 空行
1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5  ← 反応座標に入れる数値(それぞれの値で最適化する)
                                       ← 空行

この入力データを表示すると次のようになり、矢印の距離を 1.6 ～ 2.5 で動かして、それぞれの位置で最適化計算を行う。

そして、計算結果のアーカイブファイルを以下に示す。

アーカイブファイル(filename.arc) の一部

  ↓(反応座標の部分を"1.6000"にした場合の計算結果)↓
                     SUMMARY OF   PM3   CALCULATION
                                                            MOPAC  93.00
  C4  H9 
 PM3  UHF SYMMETRY
 CHPTER 10
 C2H4 + C2H5 -> C4H9

     PETERS TEST WAS SATISFIED IN BFGS OPTIMIZATION           
     SCF FIELD WAS ACHIEVED                                   

          HEAT OF FORMATION       =         6.549203 KCAL =     27.40187 KJ
          ELECTRONIC ENERGY       =     -2264.527778 EV
          CORE-CORE REPULSION     =      1652.256033 EV
          FOR REACTION COORDINATE =           1.6000 ANGSTROMS
          REACTION GRADIENT       =        41.497638 KCAL/ANGSTROM
          DIPOLE                  =         0.22003 DEBYE    SYMMETRY:       Cs  
          (SZ)                    =         0.500000
          (S**2)                  =         0.769762
          NO. OF ALPHA ELECTRONS  =        13
                                    ・
                                    ・
                                    ・
          FINAL GEOMETRY OBTAINED                                    CHARGE
 PM3  UHF SYMMETRY
 CHPTER 10
 C2H4 + C2H5 -> C4H9
  C    0.00000000  0    0.0000000  0    0.0000000  0    0    0    0     -0.2094
  C    1.46269535  1    0.0000000  0    0.0000000  0    1    0    0     -0.0704
                                    ・
  H    1.10461477  1  111.1107460  1  -59.2344276  1    8    9   10      0.0491
  H    1.10461477  0  111.1107460  0   59.2344276  0    8    9   10      0.0491
 
   4  1    5
      ・
  13 14   14
   ↓(反応座標の部分を"1.7000"にした場合の計算結果)↓
                     SUMMARY OF   PM3   CALCULATION
                                                            MOPAC  93.00
  C4  H9 
 PM3  UHF SYMMETRY
 CHPTER 10
 C2H4 + C2H5 -> C4H9

          HEAT OF FORMATION       =        12.243684 KCAL =     51.22757 KJ
          ELECTRONIC ENERGY       =     -2252.260901 EV
          CORE-CORE REPULSION     =      1640.236093 EV
          FOR REACTION COORDINATE =           1.7000 ANGSTROMS
          REACTION GRADIENT       =        68.176268 KCAL/ANGSTROM

   ↑(このまま、指定した数値について全ての計算結果と、)↑
   ↓(その時の最適化構造のデータが順に出力される。    )↓

  H    1.09796382  1  111.7910688  1   60.4212485  1    9    8    2      0.0416
  H    1.09796382  0  111.7910688  0  -60.4212485  0    9    8    2      0.0416
  H    1.08318980  1  121.1143021  1  -83.0137716  1    8    9   10      0.0823
  H    1.08318980  0  121.1143021  0   83.0137716  0    8    9   10      0.0823
 
   4  1    5
        ・
  13 14   14

この時の"HERT OF FORMATION" の値をグラフにとり極大値を遷移状態の初期構造として仮定する。また、より詳しく初期状態を求めるには、この時の結果をもとに、結合角についてもう一度反応座標を用いて計算すると良いと思われる。

最後に、最も高いエネルギーを持った構造を、mopac の入力ファイルとしてセーブする。

遷移状態の構造最適化

キーワードに「TS」を入れて計算を行う。: この時、「NLLSQ」や「SIGMA」のキーワードを入れても同様の結果が得られる。ただし、初期状態が実際の遷移状態とは大きく異なっていた場合、良い結果を得られるとは限らない。そのため、初期状態のより詳しい計算と、キーワード「TS」を推奨する。

遷移状態である事の確認

キーワードに「FORCE」を入れ、振動解析を行う。

うまく計算が出来なかった場合、以下の事を試してみると良い。 ( 他の場合にも使えます。)

この前の「TS」を入れた計算で、PRECISE」を入れて収束条件を 100倍厳しくしてみる。

「PULAY」「CAMP」「SHIFT=n」などを入れてみる。

計算結果を見て、虚の振動数を有する全対称のモードが 1つだけ存在した場合この構造は遷移状態であると初めていえる。

そのデータの一部を以下に示す。

filename.out の一部。

           NORMAL COORDINATE ANALYSIS  ←(ここから振動モードについての結果表示)
                                                   ↓
   Root No.    1       2       3       4   

              1 A'    1 A"    2 A"    2 A'  

           -574.8    58.0   140.1   196.5   ←(ここにある振動数の表示の中で
                                               マイナスのものが一つだけあれば
         1 -0.0174 -0.0001  0.0000 -0.0251     良い。マイナスが虚数を示している。)
         2  0.0000  0.0814 -0.0152  0.0001  
         3 -0.0262 -0.0001  0.0000  0.1203 
         4  0.0956  0.0000  0.0000 -0.0228  
         5 -0.0001 -0.0868 -0.0246 -0.0001  
         6 -0.2647  0.0001  0.0000 -0.1053 
         7  0.0042  0.1142  0.0062 -0.0266 
         8  0.0101  0.1545 -0.0112 -0.0019

xmol を用いて振動を確認すると良い。

目的の遷移状態である事の確認(反応物、生成物への変化の確認)

遷移状態の構造に「IRC=1」または、「IRC=-1」をいれて計算を行う。: 反応物、生成物それぞれの極小点につながる事を確認。

注意: この計算は特に計算方法(AM1,PM3,MNDO 等)に依存し、同様に計算を行っても異なる結果を得る事があります。

研究室用の説明ページへ戻る。 mopac のページへ戻る。
コメントまたはアドバイスなどがあれば以下のアドレスへどうぞ。

yagi@tube.ee.uec.ac.jp

遷移状態の計算方法の説明(TS、SADDLE)

注意