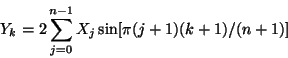 .
.Node:1d Real-odd DFTs (DSTs), Next:1d Discrete Hartley Transforms (DHTs), Previous:1d Real-even DFTs (DCTs), Up:What FFTW Really Computes
The Real-odd DFTs in FFTW are exactly equivalent to the unnormalized forward (and backward) DFTs as defined above, where the input array X of length N is purely real and is also odd. In this case, the output is odd and purely imaginary.
For the case of RODFT00, this odd symmetry means that
Xj = -XN-j,
where we take X to be periodic so that
XN = X0.
Because of this redundancy, only the first n real numbers
starting at j=1 are actually stored (the j=0 element is
zero), where N = 2(n+1).
The proper definition of odd symmetry for RODFT10,
RODFT01, and RODFT11 transforms is somewhat more intricate
because of the shifts by 1/2 of the input and/or output, although
the corresponding boundary conditions are given in Real even/odd DFTs (cosine/sine transforms). Because of the odd symmetry, however,
the cosine terms in the DFT all cancel and the remaining sine terms are
written explicitly below. This formulation often leads people to call
such a transform a discrete sine transform (DST), although it is
really just a special case of the DFT.
In each of the definitions below, we transform a real array X of length n to a real array Y of length n:
An RODFT00 transform (type-I DST) in FFTW is defined by:
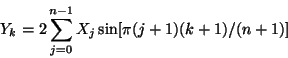 .
.An RODFT10 transform (type-II DST) in FFTW is defined by:
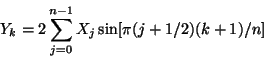 .
.An RODFT01 transform (type-III DST) in FFTW is defined by:
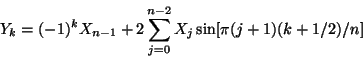 .
.An RODFT11 transform (type-IV DST) in FFTW is defined by:
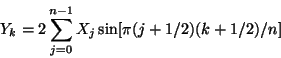 .
.These definitions correspond directly to the unnormalized DFTs used
elsewhere in FFTW (hence the factors of 2 in front of the
summations). The unnormalized inverse of RODFT00 is
RODFT00, of RODFT10 is RODFT01 and vice versa, and
of RODFT11 is RODFT11. Each unnormalized inverse results
in the original array multiplied by N, where N is the
logical DFT size. For RODFT00, N=2(n+1);
otherwise, N=2n.