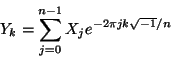Node:The 1d Real-data DFT, Next:, Previous:The 1d Discrete Fourier Transform (DFT), Up:What FFTW Really Computes


4.7.2 The 1d Real-data DFT

The real-input (r2c) DFT in FFTW computes the forward transform Y of the size n real array X, exactly as defined above, i.e.

.
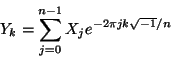This output array Y can easily be shown to possess the "Hermitian" symmetry Yk = Yn-k*, where we take Y to be periodic so that Yn = Y0.

As a result of this symmetry, half of the output Y is redundant (being the complex conjugate of the other half), and so the 1d r2c transforms only output elements 0...n/2 of Y (n/2+1 complex numbers), where the division by 2 is rounded down.

Moreover, the Hermitian symmetry implies that Y0 and, if n is even, the Yn/2 element, are purely real. So, for the R2HC r2r transform, these elements are not stored in the halfcomplex output format.

The c2r and H2RC r2r transforms compute the backward DFT of the complex array X with Hermitian symmetry, stored in the r2c/R2HC output formats, respectively, where the backward transform is defined exactly as for the complex case:

.
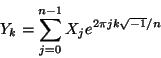The outputs Y of this transform can easily be seen to be purely real, and are stored as an array of real numbers.

Like FFTW's complex DFT, these transforms are unnormalized. In other words, applying the real-to-complex (forward) and then the complex-to-real (backward) transform will multiply the input by n.