| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
| 76.1 Introduction to orthogonal polynomials | ||
| 76.2 Functions and Variables for orthogonal polynomials |
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
orthopolyは、
Chebyshev, Laguerre, Hermite, Jacobi, Legendre,
超球 (Gegenbauer)多項式を含むいくつかの種類の直交多項式の
シンボリックな評価と数値評価のためのパッケージです。
さらに、 orthopolyは球 Bessel, 球 Hankel, 球調和関数のサポートを含みます。
ほとんどの部分に関して、 orthopolyは
Abramowitz and StegunのHandbook of Mathematical Functions, Chapter 22 (10th printing, December 1972)の慣例に従います;
加えて、
Gradshteyn and RyzhikのTable of Integrals, Series, and Products (1980 corrected and enlarged edition)と
Eugen MerzbacherのQuantum Mechanics (2nd edition, 1970)を使います。
University of Nebraska at Kearney (UNK)のBarton Willisが
orthopolyパッケージとドキュメンテーションを書きました。
パッケージは GNU General Public License (GPL)の下で公開されています。
Categories: Orthogonal polynomials · Share packages · Package orthopoly
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
load (orthopoly)は orthopolyパッケージをロードします。
3次の Legendre多項式を見つけるには、
(%i1) legendre_p (3, x);
3 2
5 (1 - x) 15 (1 - x)
(%o1) - ---------- + ----------- - 6 (1 - x) + 1
2 2
|
これを xの冪の和として表すには、 ratsimpか ratを結果に適用してください。
(%i2) [ratsimp (%), rat (%)];
3 3
5 x - 3 x 5 x - 3 x
(%o2)/R/ [----------, ----------]
2 2
|
あるいはまた、
legendre_pの第二引数 (「主」変数)を正準有理形 (CRE)にしてください。
(%i1) legendre_p (3, rat (x));
3
5 x - 3 x
(%o1)/R/ ----------
2
|
浮動小数点評価に関して、
orthopolyはランニング誤差解析を使って誤差の上限を推定します。
例えば、
(%i1) jacobi_p (150, 2, 3, 0.2); (%o1) interval(- 0.062017037936715, 1.533267919277521E-11) |
区間は interval (c, r)形を取ります。
ここで cは中央値、 rは区間の半径です。
Maximaは区間上の算術をサポートしていないので、グラフィックスなどいくつかの状況では
誤差を抑制し、区間の中央値だけ出力したいでしょう。
これをするには、オプション変数 orthopoly_returns_intervalsを
falseに設定してください。
(%i1) orthopoly_returns_intervals : false; (%o1) false (%i2) jacobi_p (150, 2, 3, 0.2); (%o2) - 0.062017037936715 |
更に知るにはセクション see Floating point Evaluationを参照してください。
orthopolyのほとんどの関数は gradefプロパティを持ちます;
例えば、
(%i1) diff (hermite (n, x), x);
(%o1) 2 n H (x)
n - 1
(%i2) diff (gen_laguerre (n, a, x), x);
(a) (a)
n L (x) - (n + a) L (x) unit_step(n)
n n - 1
(%o2) ------------------------------------------
x
|
二番目の例の単位階段関数は、 nが 0で評価することによって、そうでなければ生じる誤差を抑制します。
(%i3) ev (%, n = 0); (%o3) 0 |
gradefプロパティは「主」変数にのみ適用されます;
他の引数に関する導関数は、普通、エラーメッセージに帰着します;
例えば、
(%i1) diff (hermite (n, x), x);
(%o1) 2 n H (x)
n - 1
(%i2) diff (hermite (n, x), n);
Maxima doesn't know the derivative of hermite with respect the first
argument
-- an error. Quitting. To debug this try debugmode(true);
|
一般に orthopolyの関数はリストや行列上に写像します。
写像を完全に評価するには、
オプション変数 doallmxopsと listarithはともに
true(デフォルト値)でなければいけません。
行列上への写像を見るには以下を考えてください。
(%i1) hermite (2, x);
2
(%o1) - 2 (1 - 2 x )
(%i2) m : matrix ([0, x], [y, 0]);
[ 0 x ]
(%o2) [ ]
[ y 0 ]
(%i3) hermite (2, m);
[ 2 ]
[ - 2 - 2 (1 - 2 x ) ]
(%o3) [ ]
[ 2 ]
[ - 2 (1 - 2 y ) - 2 ]
|
二番目の例では、値の i, j要素は hermite (2, m[i,j])です;
次の例で見るように、これは計算 -2 + 4 m . mと同じではありません。
(%i4) -2 * matrix ([1, 0], [0, 1]) + 4 * m . m;
[ 4 x y - 2 0 ]
(%o4) [ ]
[ 0 4 x y - 2 ]
|
定義域外の点で関数を評価すると、一般に、
orthopolyは未評価関数を返します。
例えば、
(%i1) legendre_p (2/3, x);
(%o1) P (x)
2/3
|
orthopolyは TeXへの翻訳をサポートします;
端末上での 2次元出力も行います。
(%i1) spherical_harmonic (l, m, theta, phi);
m
(%o1) Y (theta, phi)
l
(%i2) tex (%);
$$Y_{l}^{m}\left(\vartheta,\varphi\right)$$
(%o2) false
(%i3) jacobi_p (n, a, a - b, x/2);
(a, a - b) x
(%o3) P (-)
n 2
(%i4) tex (%);
$$P_{n}^{\left(a,a-b\right)}\left({{x}\over{2}}\right)$$
(%o4) false
|
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
式がいくつかの直交多項式を記号順で含む時、 式が実際に 0になる可能性がありますが、 まだ Maximaはそれを零に整理することができません。 もしそんな量で割るなら、困ったことになるでしょう。 例えば、以下の式は 1より大きな整数 nで零になりますが、 まだ Maximaはそれを零に整理することができません。
(%i1) (2*n - 1) * legendre_p (n - 1, x) * x - n * legendre_p (n, x)
+ (1 - n) * legendre_p (n - 2, x);
(%o1) (2 n - 1) P (x) x - n P (x) + (1 - n) P (x)
n - 1 n n - 2
|
特定の nでは式を零に換算できます。
(%i2) ev (% ,n = 10, ratsimp); (%o2) 0 |
一般に、直交多項式の多項式形は浮動小数点評価に関しては不適当です。 以下は例です。
(%i1) p : jacobi_p (100, 2, 3, x)$ (%i2) subst (0.2, x, p); (%o2) 3.4442767023833592E+35 (%i3) jacobi_p (100, 2, 3, 0.2); (%o3) interval(0.18413609135169, 6.8990300925815987E-12) (%i4) float(jacobi_p (100, 2, 3, 2/10)); (%o4) 0.18413609135169 |
真値は約0.184です; この計算は極端な減算消去誤差に苦しみます。 多項式を展開し評価すると、よりよい結果を与えます。
(%i5) p : expand(p)$ (%i6) subst (0.2, x, p); (%o6) 0.18413609766122982 |
これは一般的な規則ではありません; 多項式を展開することはいつも、より数値評価に適した式を生じるわけではありません。 数値評価する最もよい方法は断然、関数引数を少なくとも1つ浮動小数点数にすることです。 それをすることで、特別な浮動小数点アルゴリズムが評価に使われます。
Maximaの float関数は幾分でたらめです;
もし
floatを記号次数や順序パラメータを持つ直交多項式を含む式に適用するなら、
これらのパラメータは浮動小数点に変換されるかもしれません;
その後、式は完全には評価されません。
以下を考えてください。
(%i1) assoc_legendre_p (n, 1, x);
1
(%o1) P (x)
n
(%i2) float (%);
1.0
(%o2) P (x)
n
(%i3) ev (%, n=2, x=0.9);
1.0
(%o3) P (0.9)
2
|
(%o3)の式は浮動小数点に評価されません;
orthopolyは整数を要求するところで浮動小数点値を認識しません。
同様に、
pochhammer_max_indexを越える位数の
pochhammer関数の数値評価はトラブルの元かもしれません;
以下を考えてください。
(%i1) x : pochhammer (1, 10), pochhammer_max_index : 5;
(%o1) (1)
10
|
floatを適用することは xを浮動小数点に評価しません。
(%i2) float (x);
(%o2) (1.0)
10.0
|
xを浮動小数点に評価するには、
pochhammer_max_indexを 11以上にバインドして、
floatを xに適用する必要があります。
(%i3) float (x), pochhammer_max_index : 11; (%o3) 3628800.0 |
pochhammer_max_indexのデフォルト値は 100です;
orthopolyをロードした後、値を変えてください。
最後に、参考書は直交多項式の定義を変えることを承知してください; 一般的に Abramowitz and Stegunの慣例を使っています。
orhtopolyのバグを疑う前にいくつかの特殊なケースをチェックして、あなたの定義が
orthopolyが使っているものと一致しているかを明らかにしてください。
定義はしばしば規格化について異なります; 時々、著者は (-1, 1)以外の区間上で直交な族を作る関数の「シフト」版を使います。 例えば、 (0, 1)上で直交するLegendre多項式を定義するのに、 以下を定義します。
(%i1) shifted_legendre_p (n, x) := legendre_p (n, 2*x - 1)$
(%i2) shifted_legendre_p (2, rat (x));
2
(%o2)/R/ 6 x - 6 x + 1
(%i3) legendre_p (2, rat (x));
2
3 x - 1
(%o3)/R/ --------
2
|
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
orthopolyの関数のほとんどは浮動小数点評価中の誤差を見積もるのに、
ランニング誤差解析を使います;
例外は球 Bessel関数と第二種 Legendreの陪多項式です。
数値評価のため、球 Bessel関数は SLATEC関数をコールします。
第二種 Legendreの陪多項式の数値評価のために特別な方法は使われません。
ランニング誤差解析は (丸め単位としても知られている)計算機イプシロンの二次か高次の誤差を無視します。 2,3の他の誤差も無視します。 (ありそうにありませんが、)実際の誤差は推定を越える可能性があります。
区間は形式 interval (c, r)を持ちます。
ここで、cは区間の中心で、 rは半径です。
区間の中心は複素数であり得ますし、
半径はいつも正の実数です。
以下は例です。
(%i1) fpprec : 50$ (%i2) y0 : jacobi_p (100, 2, 3, 0.2); (%o2) interval(0.1841360913516871, 6.8990300925815987E-12) (%i3) y1 : bfloat (jacobi_p (100, 2, 3, 1/5)); (%o3) 1.8413609135168563091370224958913493690868904463668b-1 |
実際の誤差が誤差推定よりも小さいことをテストしましょう。
(%i4) is (abs (part (y0, 1) - y1) < part (y0, 2)); (%o4) true |
なるほど、この例では、 誤差推定は真の誤差の上限です。
Maximaは区間の算術をサポートしていません。
(%i1) legendre_p (7, 0.1) + legendre_p (8, 0.1);
(%o1) interval(0.18032072148437508, 3.1477135311021797E-15)
+ interval(- 0.19949294375000004, 3.3769353084291579E-15)
|
ユーザーは区間算数を行う計算をする演算子を定義できます。 区間の足し算を定義するには、以下のように定義できます。
(%i1) infix ("@+")$
(%i2) "@+"(x,y) := interval (part (x, 1) + part (y, 1), part (x, 2)
+ part (y, 2))$
(%i3) legendre_p (7, 0.1) @+ legendre_p (8, 0.1);
(%o3) interval(- 0.019172222265624955, 6.5246488395313372E-15)
|
引数が複素数の時、特殊な浮動小数点ルーチンがコールされます。 例えば、
(%i1) legendre_p (10, 2 + 3.0*%i);
(%o1) interval(- 3.876378825E+7 %i - 6.0787748E+7,
1.2089173052721777E-6)
|
これを真値と比較しましょう。
(%i1) float (expand (legendre_p (10, 2 + 3*%i))); (%o1) - 3.876378825E+7 %i - 6.0787748E+7 |
更に、引数が多倍長浮動小数点の時、特殊な浮動小数点ルーチンがコールされます; しかしながら、多倍長浮動小数点は倍精度浮動小数点に変換され、最終結果は倍精度です。
(%i1) ultraspherical (150, 0.5b0, 0.9b0); (%o1) interval(- 0.043009481257265, 3.3750051301228864E-14) |
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
orthopoly 直交多項式を含む式をプロットするには 2つのことをしなければいけません:
orthopoly_returns_intervalsを falseに設定する。
orthopoly関数のすべてのコールをクォートする。
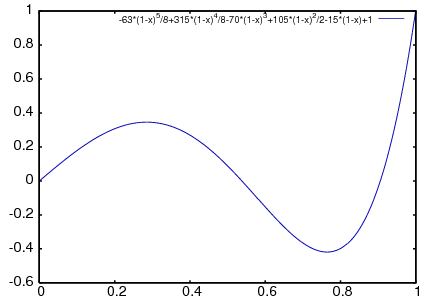
もし関数コールがクォートされていないなら、 Maximaはプロットする前にそれらを多項式に評価します; 結果として、特殊な浮動小数点コードはコールされません。 以下は、 Legendre多項式を含む式をどうやってプロットするかの例です。
(%i1) plot2d ('(legendre_p (5, x)), [x, 0, 1]),
orthopoly_returns_intervals : false;
(%o1)
|

式 legendre_p (5, x)全体をクォートします;
これは 'legendre_p (5, x)を使って関数名をクォートするだけとは違います。
Categories: Plotting
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
orthopolyパッケージは
Pochhammerシンボルと単位階段函数を定義します。
orthopolyは gradef文の中で
Kroneckerのデルタ函数と単位階段函数を使います。
Pochhammerシンボルをガンマ函数の商に変換するには、
makegammaを使ってください。
(%i1) makegamma (pochhammer (x, n));
gamma(x + n)
(%o1) ------------
gamma(x)
(%i2) makegamma (pochhammer (1/2, 1/2));
1
(%o2) ---------
sqrt(%pi)
|
Pochhammerシンボルの導函数は
psi函数を使って与えられます。
(%i1) diff (pochhammer (x, n), x);
(%o1) (x) (psi (x + n) - psi (x))
n 0 0
(%i2) diff (pochhammer (x, n), n);
(%o2) (x) psi (x + n)
n 0
|
(%o1)の式に注意する必要があります;
psi函数の差分は
x = -1, -2, .., -nの時多項式です。
これらの多項式は nが正の整数の時、導函数を
n - 1次多項式にするように、
pochhammer (x, n)の因子を相殺します。
Pochhammerシンボルはガンマ函数の商としての表現を通して負の位数で定義されます。 以下を考えてください。
(%i1) q : makegamma (pochhammer (x, n));
gamma(x + n)
(%o1) ------------
gamma(x)
(%i2) sublis ([x=11/3, n= -6], q);
729
(%o2) - ----
2240
|
代わりに、この結果を直接得ることができます。
(%i1) pochhammer (11/3, -6);
729
(%o1) - ----
2240
|
単位階段函数は左連続です; 従って、
(%i1) [unit_step (-1/10), unit_step (0), unit_step (1/10)]; (%o1) [0, 0, 1] |
もし零で左連続でも右連続でもない単位階段函数が必要なら、
signumを使って自分のものを定義してください;
例えば、
(%i1) xunit_step (x) := (1 + signum (x))/2$
(%i2) [xunit_step (-1/10), xunit_step (0), xunit_step (1/10)];
1
(%o2) [0, -, 1]
2
|
unit_step自身を再定義しないでください;
orthopolyの中のあるコードは単位階段函数が左連続であることを要求します。
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
一般的に、 orthopolyは直交多項式の超幾何表現を使うことで記号評価をします。
超幾何函数は(ドキュメント化されていない)関数 hypergeo11と
hypergeo21を使って評価されます。
例外は半整数 Bessel函数と第二種 Legendreの陪函数です。
半整数 Bessel函数は明示的な表現を使って評価されます。
第二種 Legendreの陪函数は再帰を使って評価されます。
浮動小数点評価のために、函数のほとんどを超幾何形式に再び変換します; 順方向再帰を使って超幾何函数を評価します。 ここでも、例外は半整数 Bessel函数と第二種 Legendreの陪函数です。 半整数 Bessel函数は SLATECコードを使って数値的に評価されます。
| [ < ] | [ > ] | [ << ] | [ Up ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
次数 nと位数 mの第一種Legendre陪函数。
参考文献: Abramowitz and Stegun, equations 22.5.37, page 779, 8.6.6 (second equation), page 334, and 8.2.5, page 333.
Categories: Package orthopoly
次数 nと位数 mの第二種Legendre陪函数。
参考文献: Abramowitz and Stegun, equation 8.5.3 and 8.1.8.
Categories: Package orthopoly
n次の第一種 Chebyshev多項式。
参考文献: Abramowitz and Stegun, equation 22.5.47, page 779.
Categories: Package orthopoly
n次の第二種 Chebyshev多項式。
参考文献: Abramowitz and Stegun, equation 22.5.48, page 779.
Categories: Package orthopoly
次数 nの一般化 Laguerre多項式。
参考文献: Abramowitz and Stegun, equation 22.5.54, page 780.
Categories: Package orthopoly
n次の Hermite多項式。
参考文献: Abramowitz and Stegun, equation 22.5.55, page 780.
Categories: Package orthopoly
もし入力が区間なら trueを、そうでないなら falseを返します。
Categories: Package orthopoly · Predicate functions
Jacobiの多項式。
Jacobiの多項式は実際には
aと bすべてに対して定義されます;
しかし、Jacobi多項式の重み
(1 - x)^a (1 + x)^bは
a <= -1か b <= -1で可積分でありません。
参考文献: Abramowitz and Stegun, equation 22.5.42, page 779.
Categories: Package orthopoly
n次の Laguerre多項式。
参考文献: Abramowitz and Stegun, equations 22.5.16 and 22.5.54, page 780.
Categories: Package orthopoly
n次の第一種 Legendre多項式。
参考文献: Abramowitz and Stegun, equations 22.5.50 and 22.5.51, page 779.
Categories: Package orthopoly
n次の第二種 Legendre函数。
参考文献: Abramowitz and Stegun, equations 8.5.3 and 8.1.8.
Categories: Package orthopoly
引数 argsを持つ直交函数族 fの漸化式を返します。 再帰は多項式次数に関してです。
(%i1) orthopoly_recur (legendre_p, [n, x]);
(2 n + 1) P (x) x - n P (x)
n n - 1
(%o1) P (x) = -------------------------------
n + 1 n + 1
|
orthopoly_recurの二番目の引数は
関数 fの正しい数の引数のリストでなければいけません;
もしそうでないなら Maximaはエラーをシグナルします。
(%i1) orthopoly_recur (jacobi_p, [n, x]); Function jacobi_p needs 4 arguments, instead it received 2 -- an error. Quitting. To debug this try debugmode(true); |
更に、 fが直交多項式族の1つの名前でないなら、エラーがシグナルされます。
(%i1) orthopoly_recur (foo, [n, x]); A recursion relation for foo isn't known to Maxima -- an error. Quitting. To debug this try debugmode(true); |
Categories: Package orthopoly
デフォルト値: true
orthopoly_returns_intervalsが trueの時、浮動小数点の結果が形式
interval (c, r)で返されます。
ここで、 cは区間の中心で、 rは半径です。
中心は複素数であり得ます;
その場合、区間は複素平面上の円です。
Categories: Package orthopoly
3つの要素のリストを返します; 一番目の要素はリスト argsが与える引数を持つ直交多項式族 fの重みの公式です; 二番目と三番目の要素は直交性の区間の下限と上限を与えます。 例えば、
(%i1) w : orthopoly_weight (hermite, [n, x]);
2
- x
(%o1) [%e , - inf, inf]
(%i2) integrate(w[1]*hermite(3, x)*hermite(2, x), x, w[2], w[3]);
(%o2) 0
|
fの主変数はシンボルでなければいけません; そうでないなら Maximaはエラーをシグナルします。
Categories: Package orthopoly
Pochhammerシンボル。
n <= pochhammer_max_indexの非負整数 nに対して、式
pochhammer (x, n)は
n > 0の時、積
x (x + 1) (x + 2) ... (x + n - 1)を評価します。
n = 0の時は 1です。
負の nに対しては、
pochhammer (x, n)は
(-1)^n / pochhammer (1 - x, -n)として定義されます。
従って、
(%i1) pochhammer (x, 3);
(%o1) x (x + 1) (x + 2)
(%i2) pochhammer (x, -3);
1
(%o2) - -----------------------
(1 - x) (2 - x) (3 - x)
|
Pochhammerシンボルをガンマ函数の商に変換するには、
(Abramowitz and Stegun, equation 6.1.22を参照してください)
makegammaを使ってください;
例えば、
(%i1) makegamma (pochhammer (x, n));
gamma(x + n)
(%o1) ------------
gamma(x)
|
nが pochhammer_max_indexを越えるか、
nが記号の時、
pochhammerは名詞形を返します。
(%i1) pochhammer (x, n);
(%o1) (x)
n
|
Categories: Package orthopoly · Gamma and factorial functions
デフォルト値: 100
pochhammer (n, x)は
n <= pochhammer_max_indexの時だけ
積を展開します。
例:
(%i1) pochhammer (x, 3), pochhammer_max_index : 3;
(%o1) x (x + 1) (x + 2)
(%i2) pochhammer (x, 4), pochhammer_max_index : 3;
(%o2) (x)
4
|
参考文献: Abramowitz and Stegun, equation 6.1.16, page 256.
Categories: Package orthopoly · Gamma and factorial functions
第一種球 Bessel函数。
参考文献: Abramowitz and Stegun, equations 10.1.8, page 437 and 10.1.15, page 439.
Categories: Package orthopoly · Bessel functions
第二種球 Bessel函数。
参考文献: Abramowitz and Stegun, equations 10.1.9, page 437 and 10.1.15, page 439.
Categories: Package orthopoly · Bessel functions
第一種球 Hankel函数。
参考文献: Abramowitz and Stegun, equation 10.1.36, page 439.
Categories: Package orthopoly · Bessel functions
第二種球 Hankel函数。
参考文献: Abramowitz and Stegun, equation 10.1.17, page 439.
Categories: Package orthopoly · Bessel functions
球調和函数。
参考文献: Merzbacher 9.64.
Categories: Package orthopoly
左連続の単位階段函数;なので
unit_step (x)はx <= 0で0であり、
x > 0で1です。
もし0で値1/2を取る単位階段函数が欲しいなら、
(1 + signum (x))/2を使ってください。
Categories: Package orthopoly · Mathematical functions
(Gegenbauer多項式としても知られている)超球多項式。
参考文献: Abramowitz and Stegun, equation 22.5.46, page 779.
Categories: Package orthopoly
| [ << ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
This document was generated by 市川雄二 on June, 21 2016 using texi2html 1.76.