最も強い繊維としてのカーボンナノチューブ
北陸先端科学技術大学院大学 尾崎泰助、岩佐義宏、三谷洋興
これまでの実験・理論両面における多くの精力的な研究からカーボンナノチューブが極
めて特異な力学特性を持っていることが分かってきた[4-13]。この特異な力学特性を端的に
述べれば、次の三つの観点から特徴付けられるであろう。
(1) 異方性: カーボンナノチューブの力学特性は多くの高分子繊維と同様に非常に異
方性が大きい。
(2) 硬性: 長軸方向のヤング率はダイヤモンドのそれ(≈ 1 TPa)にほぼ匹敵。
(3) 復元性: 非常に大きな曲げや歪みに対して、ほとんど欠陥を生じることなしに元
の構造に復元する。
これらの顕著な力学特性と併せ、軽元素の炭素原子のみから構成された低密度物質(1.3g/cm3)であることから、カーボンナノチューブは航空機や宇宙材料などの構造材料とし
て大きな期待が持たれている。
カーボンナノチューブの螺旋度と力学特性の関係は研究初期から大きな関心が持たれ、
すでにヤング率のような低歪み領域の力学特性は螺旋度にほとんど依存しないと理論計算
から予測されている[7-10]。弾性領域を越える大歪み領域においてはそのネットワーク構造
が大きく歪み、その結果、力学特性と螺旋度が何らかの関係を持っていると考えられるが、その詳細はこれまで明らかではない。蜂の巣格子の歪みがどのように力学特性と関連づけられるのか?、またチューブ構造と力学特性の関連など、ナノチューブの構造と力学特性の関係は電子物性とは違った観点の面白い物理を提供しているであろう。そこで今回、我々
は軸圧縮・引っ張りの大規模分子動力学シミュレーションを行ない、弾性歪み領域を越え
た大歪み領域における軸応力の螺旋度依存性をネットワークの構造から詳細に検討した[1]。
最近の強結合電子状態計算における効率的計算法の発達は数千原子を含んだ系のモデル
ポテンシャルによらない分子動力学シミュレーションを可能にした[2,3]。これはカーボン
系の多くの現象を取り扱うことのできる非常に有効な方法である。我々はこの効率的計算
法を用いて、ほぼ同径(≈13.4Å)で長さ140Åの5種類の単層ナノチューブ((10,10), (12,8),
(14,5), (16,2), (17,0))の引っ張り及び、圧縮シミュレーションを有限温度下(0, 300K)で行な
った。この大規模シミュレーションにおけるナノチューブの歪みの様子から、顕著な温度
効果が圧縮下の座屈限界歪みと、図1に示されるような座屈形態に観察された。0、300K
において5種類の単層ナノチューブは圧縮率19、10%でそれぞれ座屈し、また初期長さ
の80%におけるアームチェア(10,10)チューブにおける座屈波長はそれぞれ4.8Å 、13Å で
あった。座屈形態の温度依存性は分岐現象として非常に興味深いものであるが、300 Kでの
長距離座屈は圧縮の初期段階から局所的な歪みを解消する方向に働き、応力の螺旋度依存
|
|
図1 (10,10)単層ナノチューブの座屈形態の温度依存性。0、300Kシミュレーション
における圧縮率80% のスナップショットをそれぞれ示す。
性を不鮮明にする。そこで本研究では0Kでの座屈が起こる直前の応力の螺旋度依存性に注
目した。
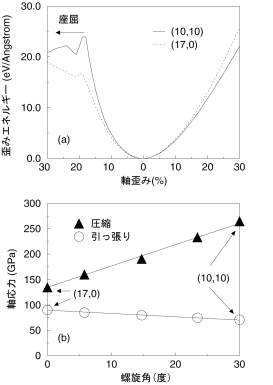
図2(a)にアームチェア(10,10)及び、ジグザグ(17,0)チューブの単位長さあたりの歪み
エネルギーを示す。この歪みエネルギー曲線から求めたアームチェア(10,10)及び、ジグザ
グ(17,0)チューブのヤング率はそれぞれ988GPa、973GPaであり、これまでの理論予測と
矛盾しない。一方、大歪み領域における歪みエネルギーは顕著に螺旋度に依存し、この時、
軸応力は螺旋角にほぼ線形に依存する(図2(b))。しかも圧縮と引っ張り下でその関係が反転
し、ほぼ同径チューブで比較すれば、それぞれアームチェア及び、ジグザグチューブが最
も堅いチューブとなることが分かった。圧縮下15%でのアームチェア(10,10)チューブの軸
応力はジグザグ(17,0)チューブのそれのおよそ2倍に達する。大歪み領域の応力の螺旋度依
存性と圧縮と引っ張り下における応力の反転現象は本研究において始めて見い出されたも
のである。図2(a)からこの軸応力の螺旋度依存性は非調和型の歪みエネルギーに起因する
ことが分かる。
そこで次にアームチェア(10,10)及び、ジグザグ(17,0)チューブの非調和型の歪みエネルギ
ーの物理的な起源を考える。まず始めに非調和型の歪みエネルギーに対するネットワーク
構造とチューブ構造の寄与を分離するため、グラファイトシートの歪みエネルギーをナノ
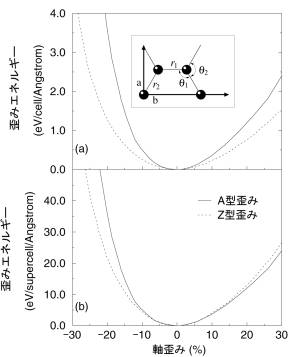
チューブのそれと比較した。図3(a)に単位長さ・単位格子あたりのグラファイトシートの
歪みエネルギーを示す。ここで単位格子は図3(a)中に示されたように4つの炭素原子を含
み、直交化された単位ベクトルの長さは|a|=2r2sinq1及び、|b|=2r1 - 2r2cosq1でそれぞれ
与えられる。また2種の歪み、A型歪みとZ型歪みはアームチェア及び、ジグザグチュー
|
|
|
|
図2 (a) 0Kシミュレーションにおける 図3 (a) A型歪み及び、Z型歪みに対す
アームチェア(10,10)とジグザグ(17,0)単層 るグラファイトシートの単位格子・単位
カーボンナノチューブの歪みエネルギー。 長さあたりの歪みエネルギー。(b) アー
(b) ほぼ同一の直径を持った単層カーボン チェア(10,10)とジグザグチューブ(17,0)
ナノチューブの0Kでの圧縮・引っ張り下 グラファイト展開格子に対するA型歪み
(15%)の応力。 とZ型歪みの単位長さあたりの歪みエネ
ルギー。
ブの軸方向に対応する歪みである。図3(a)より単位長さ・単位格子あたりで考えた場合、
A型歪みの歪みエネルギーが常に大きいことが分かる。アームチェア(10,10)及び、ジグザグ(17,0)チューブの展開図に対応するグラファイトシートの歪みエネルギーは図3(a)のA型
歪み及び、Z型歪みの歪みエネルギーにそれぞれ10及び、17倍することによって得られる
(図3(b))。図2(a)と図3(b)の比較から、アームチェア(10,10)及び、ジグザグ(17,0)チューブ
の歪みエネルギーはチューブ構造よりむしろ、そのネットワーク構造に由来していると結論付けられる。したがって、単層ナノチューブの非調和的な歪みエネルギーは六員環の歪
みエネルギーの方向依存性とチューブ上の六員環の数の二つの因子によって決定されてい
ることが分かる。
さらに我々は結合長と結合角の歪みに対して調和ポテンシャルを仮定した単純な調和ポ
テンシャルと強結合モデルの2次モーメント近似から導かれる解析的ボンドオーダーポテ
|
|
ンシャル(BOP)[14]を用いて、単位格子の歪みエネルギーを個々の結合長及び、結合角の歪みと関連付けた。歪みエネルギーにおける結合長及び、結合角の歪みの寄与を分離するため、結合長固定及び、結合角固定の2つの制約条件下でこれらの二つのポテンシャルを解析した。
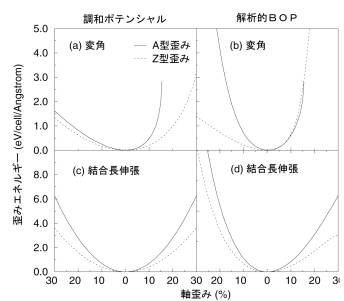
図4(a)と(b)はそれぞれ結合長固定下における調和ポテンシャル及び、解析的BOPの歪みエネルギーを示す。A型歪みの圧縮下及び、Z型歪みの引っ張り下において解析的BOPによる歪みエネルギーが著しく増大していることが分かる。 図4 二つのモデルポテンシャル(調和ポテンシャ
解析的BOPにおいて歪みエネルギ ル、解析的BOP)によるA型歪み及び、Z型歪み
ーはσ及び、πボンドエネルギーと に対するグラファイトシートの単位格子・単位長
反発エネルギーからの寄与を持って さあたりの歪みエネルギー。(a)、(b)、(c)、及び(d)
いるが、結合長固定下ではπボンド はそれぞれ結合長固定と結合角固定における調和
エネルギーと第一隣接原子間の反発 ポテンシャルと解析的BOPの歪みエネルギーを
エネルギーは不変であるので、歪み を示す。
エネルギーはσボンドエネルギーと
第二隣接原子間の反発エネルギーのみの寄与を持つ。第二隣接原子間の反発エネルギーを
含めない場合、その歪みエネルギーは調和ポテンシャルのそれに非常に良く類似し、σボ
ンドエネルギーの角度依存性は意外にも、ほぼ調和ポテンシャルで近似できることが分か
った。したがって、図4(a)と(b)のA型歪みの圧縮下及び、Z型歪みの引っ張り下の歪みエ
ネルギーの増大は第二隣接原子間の反発エネルギーのためである。
図4(c)と(d)はそれぞれ結合角固定下における調和ポテンシャル及び、解析的BOPの歪み
エネルギーを示す。調和ポテンシャルの歪みエネルギーは完全に調和的であるが、 解析的
BOPのそれは引っ張り下、歪みエネルギーが大きく増大しない。この非調和的な振舞いは
図3(a)に良く類似し、このことから結合長由来の歪みエネルギーによって、六員環の歪み
エネルギーの非調和性がほぼ決定されていることが分かる。
この結合長固定・結合角固定による解析から、グラファイト格子のA型歪み及び、Z型
歪みに対する非調和的な振舞いに対し、一つの明確な説明が可能である。すなわち、図3(a)
の歪みエネルギーにおける非調和性はその大部分は結合角の歪みによるものより、むしろ結合長の伸長に由来する。言い替えれば、グラファイトシートは外力に対して、結合長の
伸長を優先させ変形する。さらにこの結合長由来の歪みエネルギーに修正を加える形で、
結合角の歪みによる寄与が加わる。Z型歪みの場合、圧縮下における結合角変位の歪みエネ
ルギーが小さく、結合角と結合長の変位を伴った変形が起こる。この違いはA型歪みとZ型歪みにおける第2隣接原子間の反発エネルギーの寄与に帰することができる。その結果として、単層ナノチューブの大歪み領域における軸応力の螺旋度依存性の反転現象が引き
起こされる。
以上をまとめる。我々がこれまで開発してきた効率的計算法を用いて、単層ナノチューブの大規模な軸圧縮・引っ張りシミュレーションを行なった。その結果、大歪み領域にお
いて0K応力が単層ナノチューブの螺旋角にほぼ線形に依存し、圧縮に対してアームチェ
アチューブが、引っ張りに対してジグザグチューブが最も堅いチューブであることが分か
った。グラファイトシートの歪みエネルギーとの比較から、この特異な力学特性がチュー
ブ構造よりむしろネットワーク構造に由来していることが分かった。さらに二つのモデルポテンシャルによるグラファイトシートの歪みエネルギーの解析から、この非調和的歪み
エネルギーの物理的起源に対する一つの解釈が得られた。したがって、我々は大歪み領域
の単層ナノチューブの力学的な性質は顕著にそのネットワーク構造を反映したものである
と結論する。グラファイトシートでも同様の力学特性が現れると考えられるがナノチュー
ブの特異性は螺旋角を調節することにより、まさにグラファイトシートを任意の方向に圧
縮・引っ張りできることにあるだろう。
今後、本理論的予測が実験によって確認されることを強く期待する。
[参考文献]
[1]
T. Ozaki, Y.
Iwasa, and T.Mitani,Phys. Rev. Lett. 84, 1712 (2000).
[2]
T. Ozaki,
Phys. Rev. B 59, 16061 (1999).
[3]
T. Ozaki, M.
Aoki, and D. G. Pettifor, Phys. Rev. B 61,
7972 (2000).
[4]
S. Iijima, C.
Brabec, A. Maiti, and J. Bernholc, J. Chem. Phys. 104, 2089 (1996).
[5]
M. R. Falvo,
G. J. Clary, R. M. Taylor II, V. Chi, F. P. Brooks Jr, S. Washburn,
and R. Superfine, Nature 389, 582 (1997).
[6]
Jean-Paul
Salvetat et al., Phys. Rev. Lett. 82,
944 (1999).
[7]
G. Adams et
al., Science 256, 1792 (1992).
[8]
D. Robertson,
D. Brenner, and J. Mintmire, Phys. Rev. B 45,
12592 (1992).
[9] A. Lucas, P. Lambin, and
R. Smally, J. Phys. Chem. Solids 54,
587 (1993).
[10]
J. P. Lu, Phys. Rev. Lett. 79, 1297 (1997).
[11]
B. I. Yakobson, C. J. Brabec, and J.
Bernholc, Phys. Rev. Lett. 76, 2511
(1996).
[12]
P. Zhang, P. E. Lammert, and V. H.
Crespi, Phys. Rev. Lett. 81, 5346
(1998).
[13]
D. Srivastava, M. Menon, and K. Cho,
Phys. Rev. Lett. 83, 2973 (1999).
[14]
D. G. Pettifor and I. I. Oleinik, Phys.
Rev. B 59, 8487(1999);
I.
I. Oleinik
and D. G. Pettifor, Phys. Rev. B 59,
8500(1999) and references
therein.