61. graphs

[ < ]

[ > ]

[ << ]

[ Up ]

[ >> ]

[Top]

[Contents]

[Index]

[ ? ]

61.1 Introduction to graphs

graphsパッケージは Maximaに無向グラフ (以下グラフ)とダイグラフ(以下ダイグラフ)のデータ構造を提供します。ダイグラフは uから vへの有向辺と vから uへの有向辺を持つことがありますが、グラフやダイグラフは単純です(多重辺もループも持ちません)。

内部的にはグラフは隣接リストで表現され、 lisp構造として実装されます。頂点はそれらの id (idは整数)で識別されます。辺/弧は長さ 2のリストで表現されます。グラフ/ダイグラフの頂点にラベルを割り当てることができ、グラフ/ダイグラフの辺/弧に重みを割り当てることができます。

グラフを描画するための draw_graph関数があります。グラフは頂点配置アルゴリズムを使って描画されます。 draw_graphは http://www.graphviz.orgから入手可能な graphvizプログラムを使うこともできます。 draw_graphは Maxima drawパッケージに基づいています。

graphsパッケージを使うには最初に load(graphs)でロードしてください。

Categories: Share packages · Package graphs

[ < ]

[ > ]

[ << ]

[ Up ]

[ >> ]

[Top]

[Contents]

[Index]

[ ? ]

61.2 Functions and Variables for graphs

[ < ]

[ > ]

[ << ]

[ Up ]

[ >> ]

[Top]

[Contents]

[Index]

[ ? ]

61.2.1 Building graphs

関数: create_graph
    create_graph (v_list, e_list)
    create_graph (n, e_list)
    create_graph (v_list, e_list, directed)

頂点の集合 v_list上に辺 e_listを使って新しいグラフを生成します。

v_listは頂点のリスト ([v1, v2,..., vn])もしくは頂点ラベルを持つ頂点のリスト ([[v1,l1], [v2,l2],..., [vn,ln]])です。

nは頂点の数です。頂点は 0から n-1までの整数で識別されます。 (訳注: 1から始まる Maximaのリストの添字の慣例とは異なることに注意してください。)

e_listは辺のリスト ([e1, e2,..., em])もしくは辺の重みを持つ辺のリスト ([[e1, w1], ..., [em, wm]])です。

もし directedが falseでないならダイグラフを返します。

例1: 頂点 3つの循環を生成する。

(%i1) load (graphs)$
(%i2) g : create_graph([1,2,3], [[1,2], [2,3], [1,3]])$
(%i3) print_graph(g)$
Graph on 3 vertices with 3 edges.
Adjacencies:
  3 :  1  2
  2 :  3  1
  1 :  3  2

例2: 辺の重みを持つ頂点 3つの循環を生成する。

(%i1) load (graphs)$
(%i2) g : create_graph([1,2,3], [[[1,2], 1.0], [[2,3], 2.0],
                          [[1,3], 3.0]])$
(%i3) print_graph(g)$
Graph on 3 vertices with 3 edges.
Adjacencies:
  3 :  1  2
  2 :  3  1
  1 :  3  2

例3: ダイグラフを生成する:

(%i1) load (graphs)$
(%i2) d : create_graph(
        [1,2,3,4],
        [
         [1,3], [1,4],
         [2,3], [2,4]
        ],
        'directed = true)$
(%i3) print_graph(d)$
Digraph on 4 vertices with 4 arcs.
Adjacencies:
  4 :
  3 :
  2 :  4  3
  1 :  4  3

Categories: Package graphs

関数: copy_graph (g)

グラフ gのコピーを返します。

Categories: Package graphs · Package graphs - constructions

関数: circulant_graph (n, d)

パラメータ nと dを持つ巡回グラフを返します。

例:

(%i1) load (graphs)$
(%i2) g : circulant_graph(10, [1,3])$
(%i3) print_graph(g)$
Graph on 10 vertices with 20 edges.
Adjacencies:
  9 :  2  6  0  8
  8 :  1  5  9  7
  7 :  0  4  8  6
  6 :  9  3  7  5
  5 :  8  2  6  4
  4 :  7  1  5  3
  3 :  6  0  4  2
  2 :  9  5  3  1
  1 :  8  4  2  0
  0 :  7  3  9  1

Categories: Package graphs · Package graphs - constructions

関数: clebsch_graph ()

Clebschグラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: complement_graph (g)

グラフ gの補グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: complete_bipartite_graph (n, m)

n+mこの頂点上の完全二部グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: complete_graph (n)

nこの頂点上の完全グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: cycle_digraph (n)

n個の頂点上のダイグラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: cycle_graph (n)

nこの頂点上の閉路を返します。

Categories: Package graphs · Package graphs - constructions

関数: cuboctahedron_graph (n)

立方八面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: cube_graph (n)

n次元立方体を返します。

Categories: Package graphs · Package graphs - constructions

関数: dodecahedron_graph ()

十二面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: empty_graph (n)

n個の頂点上の空グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: flower_snark (n)

4n個の頂点上の花グラフを返します。

例:

(%i1) load (graphs)$
(%i2) f5 : flower_snark(5)$
(%i3) chromatic_index(f5);
(%o3)                           4

Categories: Package graphs · Package graphs - constructions

関数: from_adjacency_matrix (A)

隣接行列 Aで表現されるグラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: frucht_graph ()

Fruchtグラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: graph_product (g1, g1)

グラフ g1と g2の直積を返します。

例:

(%i1) load (graphs)$
(%i2) grid : graph_product(path_graph(3), path_graph(4))$
(%i3) draw_graph(grid)$

Categories: Package graphs · Package graphs - constructions

figures/graphs01

関数: graph_union (g1, g1)

グラフ g1と g2の和を返します。

Categories: Package graphs · Package graphs - constructions

関数: grid_graph (n, m)

n x mグリッドを返します。

Categories: Package graphs · Package graphs - constructions

関数: great_rhombicosidodecahedron_graph ()

大菱形二十・十二面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: great_rhombicuboctahedron_graph ()

大斜方立方八面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: grotzch_graph ()

Grotzchグラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: heawood_graph ()

Heawoodグラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: icosahedron_graph ()

二十面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: icosidodecahedron_graph ()

二十・十二面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: induced_subgraph (V, g)

グラフ gの頂点の部分集合 V上の誘導部分グラフを返します。

例:

(%i1) load (graphs)$
(%i2) p : petersen_graph()$
(%i3) V : [0,1,2,3,4]$
(%i4) g : induced_subgraph(V, p)$
(%i5) print_graph(g)$
Graph on 5 vertices with 5 edges.
Adjacencies:
  4 :  3  0
  3 :  2  4
  2 :  1  3
  1 :  0  2
  0 :  1  4

Categories: Package graphs · Package graphs - constructions

関数: line_graph (g)

グラフ gの折れ線グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: make_graph
make_graph (vrt, f)
make_graph (vrt, f, oriented)

述語論理関数 fを使ってグラフを生成します。

vrtは頂点か整数のリスト/集合です。もし vrtが整数なら、グラフの頂点は 1から vrtまでの整数です。

fは述語論理関数です。もし f(a,b)=trueなら 2つの頂点 aと bを結合します。

もし directedが falseでないならグラフは有向です。

例 1:

(%i1) load(graphs)$
(%i2) g : make_graph(powerset({1,2,3,4,5}, 2), disjointp)$
(%i3) is_isomorphic(g, petersen_graph());
(%o3)                         true
(%i4) get_vertex_label(1, g);
(%o4)                        {1, 2}

例 2:

(%i1) load(graphs)$
(%i2) f(i, j) := is (mod(j, i)=0)$
(%i3) g : make_graph(20, f, directed=true)$
(%i4) out_neighbors(4, g);
(%o4)                    [8, 12, 16, 20]
(%i5) in_neighbors(18, g);
(%o5)                    [1, 2, 3, 6, 9]

Categories: Package graphs · Package graphs - constructions

関数: mycielski_graph (g)

グラフ gの Mycielskiグラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: new_graph ()

頂点も辺も持たないグラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: path_digraph (n)

n個の頂点上の有向道を返します。

Categories: Package graphs · Package graphs - constructions

関数: path_graph (n)

n個の頂点上の道を返します。

Categories: Package graphs · Package graphs - constructions

関数: petersen_graph
petersen_graph ()
petersen_graph (n, d)

Petersenグラフ P_{n,d}を返します。 nと dのデフォルト値は n=5と d=2です。

Categories: Package graphs · Package graphs - constructions

関数: random_bipartite_graph (a, b, p)

a+b個の頂点上のランダムな2部グラフを返します。辺それぞれは確率 pで存在します。

Categories: Package graphs · Package graphs - constructions

関数: random_digraph (n, p)

n個の頂点上のランダムなダイグラフを返します。弧それぞれは確率 pで存在します。

Categories: Package graphs · Package graphs - constructions

関数: random_regular_graph
random_regular_graph (n)
random_regular_graph (n, d)

n個の頂点上のランダムな d正則グラフを返します。 dのデフォルト値は d=3です。

Categories: Package graphs · Package graphs - constructions

関数: random_graph (n, p)

n個の頂点上のランダムグラフを返します。辺それぞれは確率 pで存在します。

Categories: Package graphs · Package graphs - constructions

関数: random_graph1 (n, m)

n個の頂点とランダムな m個の辺上のランダムグラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: random_network (n, p, w)

n個の頂点上のランダムネットワークを返します。弧それぞれは確率 pで存在し、範囲 [0,w]の中に重みを持ちます。関数はリスト [network, source, sink]を返します。

例:

(%i1) load (graphs)$
(%i2) [net, s, t] : random_network(50, 0.2, 10.0);
(%o2)                   [DIGRAPH, 50, 51]
(%i3) max_flow(net, s, t)$
(%i4) first(%);
(%o4)                   27.65981397932507

Categories: Package graphs · Package graphs - constructions

関数: random_tournament (n)

n個の頂点上のランダムなトーナメントを返します。

Categories: Package graphs · Package graphs - constructions

関数: random_tree (n)

n個の頂点上のランダムな木を返します。

Categories: Package graphs · Package graphs - constructions

関数: small_rhombicosidodecahedron_graph ()

斜方二十・十二面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: small_rhombicuboctahedron_graph ()

斜方立方八面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: snub_cube_graph ()

変形立方体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: snub_dodecahedron_graph ()

変形十二面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: truncated_cube_graph ()

切頂六面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: truncated_dodecahedron_graph ()

切頂十二面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: truncated_icosahedron_graph ()

切頂二十面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: truncated_tetrahedron_graph ()

切頂四面体グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: tutte_graph ()

Tutteグラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: underlying_graph (g)

ダイグラフ gの台グラフを返します。

Categories: Package graphs · Package graphs - constructions

関数: wheel_graph (n)

n+1個の頂点上の車輪グラフを返します。

Categories: Package graphs · Package graphs - constructions

[ < ]

[ > ]

[ << ]

[ Up ]

[ >> ]

[Top]

[Contents]

[Index]

[ ? ]

61.2.2 Graph properties

関数: adjacency_matrix (gr)

グラフ grの隣接行列を返します。

例:

(%i1) load (graphs)$
(%i2) c5 : cycle_graph(4)$
(%i3) adjacency_matrix(c5);
                         [ 0  1  0  1 ]
                         [            ]
                         [ 1  0  1  0 ]
(%o3)                    [            ]
                         [ 0  1  0  1 ]
                         [            ]
                         [ 1  0  1  0 ]

Categories: Package graphs · Package graphs - properties

関数: average_degree (gr)

グラフ grに関する平均次数を返します。

例:

(%i1) load (graphs)$
(%i2) average_degree(grotzch_graph());
                               40
(%o2)                          --
                               11

Categories: Package graphs · Package graphs - properties

関数: biconnected_components (gr)

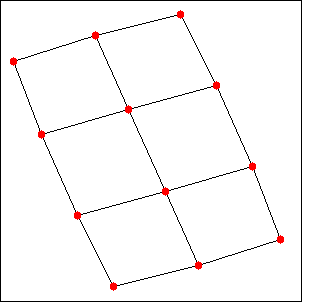
グラフ grの2連結成分(の頂点集合)を返します

例:

(%i1) load (graphs)$
(%i2) g : create_graph(
            [1,2,3,4,5,6,7],
            [
             [1,2],[2,3],[2,4],[3,4],
             [4,5],[5,6],[4,6],[6,7]
            ])$
(%i3) biconnected_components(g);
(%o3)        [[6, 7], [4, 5, 6], [1, 2], [2, 3, 4]]

figures/graphs13

Categories: Package graphs · Package graphs - properties

関数: bipartition (gr)

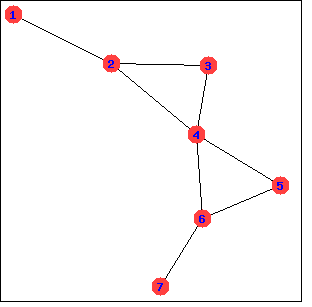
グラフ grの頂点の二分割か、もし grが二部でないなら空のリストを返します。

例:

(%i1) load (graphs)$
(%i2) h : heawood_graph()$
(%i3) [A,B]:bipartition(h);
(%o3)  [[8, 12, 6, 10, 0, 2, 4], [13, 5, 11, 7, 9, 1, 3]]
(%i4) draw_graph(h, show_vertices=A, program=circular)$

Categories: Package graphs · Package graphs - properties

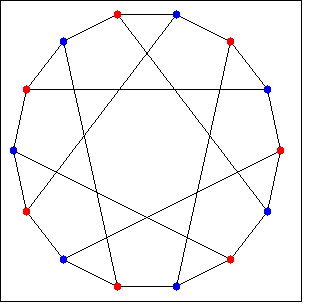
figures/graphs02

関数: chromatic_index (gr)

グラフ grの彩色指数を返します。

例:

(%i1) load (graphs)$
(%i2) p : petersen_graph()$
(%i3) chromatic_index(p);
(%o3)                           4

Categories: Package graphs · Package graphs - properties

関数: chromatic_number (gr)

グラフ grの彩色数を返します。

例:

(%i1) load (graphs)$
(%i2) chromatic_number(cycle_graph(5));
(%o2)                           3
(%i3) chromatic_number(cycle_graph(6));
(%o3)                           2

Categories: Package graphs · Package graphs - properties

関数: clear_edge_weight (e, gr)

グラフ grの辺 eの重みを削除します。

例:

(%i1) load (graphs)$
(%i2) g : create_graph(3, [[[0,1], 1.5], [[1,2], 1.3]])$
(%i3) get_edge_weight([0,1], g);
(%o3)                          1.5
(%i4) clear_edge_weight([0,1], g)$
(%i5) get_edge_weight([0,1], g);
(%o5)                           1

Categories: Package graphs · Package graphs - properties

関数: clear_vertex_label (v, gr)

グラフ grの頂点 vのラベルを削除します。

例:

(%i1) load (graphs)$
(%i2) g : create_graph([[0,"Zero"], [1, "One"]], [[0,1]])$
(%i3) get_vertex_label(0, g);
(%o3)                         Zero
(%i4) clear_vertex_label(0, g);
(%o4)                         done
(%i5) get_vertex_label(0, g);
(%o5)                         false

Categories: Package graphs · Package graphs - properties

関数: connected_components (gr)

グラフ grの連携成分(の頂点集合)を返します。

例:

(%i1) load (graphs)$
(%i2) g: graph_union(cycle_graph(5), path_graph(4))$
(%i3) connected_components(g);
(%o3)            [[1, 2, 3, 4, 0], [8, 7, 6, 5]]

Categories: Package graphs · Package graphs - properties

関数: diameter (gr)

グラフ grの直径を返します。

例:

(%i1) load (graphs)$
(%i2) diameter(dodecahedron_graph());
(%o2)                           5

Categories: Package graphs · Package graphs - properties

関数: edge_coloring (gr)

グラフ grの辺の最適色づけを返します。

関数は彩色指数と grの辺の色付けを表すリストを返します。

例:

(%i1) load (graphs)$
(%i2) p : petersen_graph()$
(%i3) [ch_index, col] : edge_coloring(p);
(%o3) [4, [[[0, 5], 3], [[5, 7], 1], [[0, 1], 1], [[1, 6], 2],
[[6, 8], 1], [[1, 2], 3], [[2, 7], 4], [[7, 9], 2], [[2, 3], 2],
[[3, 8], 3], [[5, 8], 2], [[3, 4], 1], [[4, 9], 4], [[6, 9], 3],
[[0, 4], 2]]]
(%i4) assoc([0,1], col);
(%o4)                           1
(%i5) assoc([0,5], col);
(%o5)                           3

Categories: Package graphs · Package graphs - properties

関数: degree_sequence (gr)

グラフ grの頂点次数のリストを返します。

例:

(%i1) load (graphs)$
(%i2) degree_sequence(random_graph(10, 0.4));
(%o2)            [2, 2, 2, 2, 2, 2, 3, 3, 3, 3]

Categories: Package graphs · Package graphs - properties

関数: edge_connectivity (gr)

グラフ grの辺連結性を返します。

min_edge_cutも参照してください。

Categories: Package graphs · Package graphs - properties

関数: edges (gr)

(有向)グラフ grの辺(弧)のリストを返します。

例:

(%i1) load (graphs)$
(%i2) edges(complete_graph(4));
(%o2)   [[2, 3], [1, 3], [1, 2], [0, 3], [0, 2], [0, 1]]

Categories: Package graphs · Package graphs - properties

関数: get_edge_weight
get_edge_weight (e, gr)
get_edge_weight (e, gr, ifnot)

グラフ grの辺 eの重みを返します。

もし辺に割り当てられた重みがないなら、関数は 1を返します。もし辺がグラフの中に存在しないなら、関数はエラーをシグナルするか、オプション引数 ifnotを返します。

例:

(%i1) load (graphs)$
(%i2) c5 : cycle_graph(5)$
(%i3) get_edge_weight([1,2], c5);
(%o3)                           1
(%i4) set_edge_weight([1,2], 2.0, c5);
(%o4)                         done
(%i5) get_edge_weight([1,2], c5);
(%o5)                          2.0

Categories: Package graphs · Package graphs - properties

関数: get_vertex_label (v, gr)

グラフ grの頂点 vのラベルを返します。

例:

(%i1) load (graphs)$
(%i2) g : create_graph([[0,"Zero"], [1, "One"]], [[0,1]])$
(%i3) get_vertex_label(0, g);
(%o3)                         Zero

Categories: Package graphs · Package graphs - properties

関数: graph_charpoly (gr, x)

グラフ grの(変数 xに関する)特性多項式を返します。

例:

(%i1) load (graphs)$
(%i2) p : petersen_graph()$
(%i3) graph_charpoly(p, x), factor;
                                   5        4
(%o3)               (x - 3) (x - 1)  (x + 2)

Categories: Package graphs · Package graphs - properties

関数: graph_center (gr)

グラフ grの中心を返します。

例:

(%i1) load (graphs)$
(%i2) g : grid_graph(5,5)$
(%i3) graph_center(g);
(%o3)                         [12]

Categories: Package graphs · Package graphs - properties

関数: graph_eigenvalues (gr)

グラフ grの固有値を返します。関数は maxima eigenvalues関数と同じフォーマットで固有値を返します。

例:

(%i1) load (graphs)$
(%i2) p : petersen_graph()$
(%i3) graph_eigenvalues(p);
(%o3)               [[3, - 2, 1], [1, 4, 5]]

Categories: Package graphs · Package graphs - properties

関数: graph_periphery (gr)

グラフ grの外周を返します。

例:

(%i1) load (graphs)$
(%i2) g : grid_graph(5,5)$
(%i3) graph_periphery(g);
(%o3)                    [24, 20, 4, 0]

Categories: Package graphs · Package graphs - properties

関数: graph_size (gr)

グラフ grの辺の数を返します。

例:

(%i1) load (graphs)$
(%i2) p : petersen_graph()$
(%i3) graph_size(p);
(%o3)                          15

Categories: Package graphs · Package graphs - properties

関数: graph_order (gr)

グラフ grの頂点の数を返します。

例:

(%i1) load (graphs)$
(%i2) p : petersen_graph()$
(%i3) graph_order(p);
(%o3)                          10

Categories: Package graphs · Package graphs - properties

関数: girth (gr)

grの最短閉路の長さを返します。

例:

(%i1) load (graphs)$
(%i2) g : heawood_graph()$
(%i3) girth(g);
(%o3)                           6

Categories: Package graphs · Package graphs - properties

関数: hamilton_cycle (gr)

グラフ grの Hamilton閉路を返します。もし grがハミルトニアンでないなら空のリストを返します。

例:

(%i1) load (graphs)$
(%i2) c : cube_graph(3)$
(%i3) hc : hamilton_cycle(c);
(%o3)              [7, 3, 2, 6, 4, 0, 1, 5, 7]
(%i4) draw_graph(c, show_edges=vertices_to_cycle(hc))$

Categories: Package graphs · Package graphs - properties

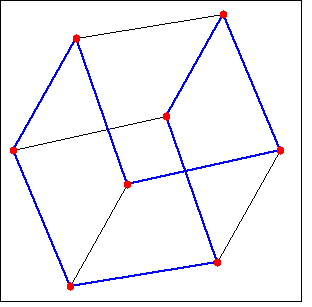
figures/graphs03

関数: hamilton_path (gr)

グラフ grの Hamilton経路を返します。もし grが Hamilton経路を持たないなら空のリストを返します。

例:

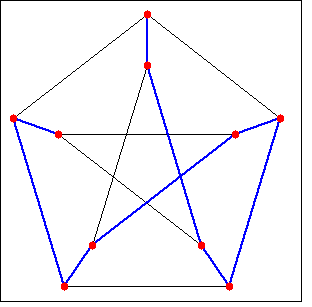
(%i1) load (graphs)$
(%i2) p : petersen_graph()$
(%i3) hp : hamilton_path(p);
(%o3)            [0, 5, 7, 2, 1, 6, 8, 3, 4, 9]
(%i4) draw_graph(p, show_edges=vertices_to_path(hp))$

Categories: Package graphs · Package graphs - properties

figures/graphs04

関数: isomorphism (gr1, gr2)

グラフ/ダイグラフ gr1と gr2の間の同型写像を返します。もし gr1と gr2が同型でないなら、空のリストを返します。

例:

(%i1) load (graphs)$
(%i2) clk5:complement_graph(line_graph(complete_graph(5)))$
(%i3) isomorphism(clk5, petersen_graph());
(%o3) [9 -> 0, 2 -> 1, 6 -> 2, 5 -> 3, 0 -> 4, 1 -> 5, 3 -> 6,
                                          4 -> 7, 7 -> 8, 8 -> 9]

Categories: Package graphs · Package graphs - properties

関数: in_neighbors (v, gr)

ダイグラフ grの頂点 vの内隣接点のリストを返します。

例:

(%i1) load (graphs)$
(%i2) p : path_digraph(3)$
(%i3) in_neighbors(2, p);
(%o3)                          [1]
(%i4) out_neighbors(2, p);
(%o4)                          []

Categories: Package graphs · Package graphs - properties

関数: is_biconnected (gr)

もし grが二連結なら trueを、そうでないなら falseを返します。

例:

(%i1) load (graphs)$
(%i2) is_biconnected(cycle_graph(5));
(%o2)                         true
(%i3) is_biconnected(path_graph(5));
(%o3)                         false

Categories: Package graphs · Package graphs - properties

関数: is_bipartite (gr)

もし grが二部(二彩色)なら trueを、そうでないなら falseを返します。

例:

(%i1) load (graphs)$
(%i2) is_bipartite(petersen_graph());
(%o2)                         false
(%i3) is_bipartite(heawood_graph());
(%o3)                         true

Categories: Package graphs · Package graphs - properties

関数: is_connected (gr)

もしグラフ grが連結なら trueを、そうでないなら falseを返します。

例:

(%i1) load (graphs)$
(%i2) is_connected(graph_union(cycle_graph(4), path_graph(3)));
(%o2)                         false

Categories: Package graphs · Package graphs - properties

関数: is_digraph (gr)

もし grがダイグラフなら trueを、そうでないなら falseを返します。

例:

(%i1) load (graphs)$
(%i2) is_digraph(path_graph(5));
(%o2)                         false
(%i3) is_digraph(path_digraph(5));
(%o3)                         true

Categories: Package graphs · Package graphs - properties

関数: is_edge_in_graph (e, gr)

もし eが(有向)グラフ gの辺(弧)なら trueを、そうでないなら falseを返します。

例:

(%i1) load (graphs)$
(%i2) c4 : cycle_graph(4)$
(%i3) is_edge_in_graph([2,3], c4);
(%o3)                         true
(%i4) is_edge_in_graph([3,2], c4);
(%o4)                         true
(%i5) is_edge_in_graph([2,4], c4);
(%o5)                         false
(%i6) is_edge_in_graph([3,2], cycle_digraph(4));
(%o6)                         false

Categories: Package graphs · Package graphs - properties

関数: is_graph (gr)

もし grがグラフなら trueを、そうでないなら falseを返します。

例:

(%i1) load (graphs)$
(%i2) is_graph(path_graph(5));
(%o2)                         true
(%i3) is_graph(path_digraph(5));
(%o3)                         false

Categories: Package graphs · Package graphs - properties

関数: is_graph_or_digraph (gr)

もし grがグラフかダイグラフなら trueを、そうでないなら falseを返します。

例:

(%i1) load (graphs)$
(%i2) is_graph_or_digraph(path_graph(5));
(%o2)                         true
(%i3) is_graph_or_digraph(path_digraph(5));
(%o3)                         true

Categories: Package graphs · Package graphs - properties

関数: is_isomorphic (gr1, gr2)

もしグラフ/ダイグラフ gr1と gr2が同型なら trueを、そうでないなら falseを返します。

isomorphismも参照してください。

例:

(%i1) load (graphs)$
(%i2) clk5:complement_graph(line_graph(complete_graph(5)))$
(%i3) is_isomorphic(clk5, petersen_graph());
(%o3)                         true

Categories: Package graphs · Package graphs - properties

関数: is_planar (gr)

もし grが平面グラフなら trueを、そうでないなら falseを返します。

使われているアルゴリズムはDemoucronのアルゴリズムです。これは二次時間アルゴリズムです。

例:

(%i1) load (graphs)$
(%i2) is_planar(dodecahedron_graph());
(%o2)                         true
(%i3) is_planar(petersen_graph());
(%o3)                         false
(%i4) is_planar(petersen_graph(10,2));
(%o4)                         true

Categories: Package graphs · Package graphs - properties

関数: is_sconnected (gr)

もしダイグラフ grが強連結なら trueを、そうでないなら falseを返します。

例:

(%i1) load (graphs)$
(%i2) is_sconnected(cycle_digraph(5));
(%o2)                         true
(%i3) is_sconnected(path_digraph(5));
(%o3)                         false

Categories: Package graphs · Package graphs - properties

関数: is_vertex_in_graph (v, gr)

もし vがグラフ gの頂点なら trueを、そうでないなら falseを返します。

例:

(%i1) load (graphs)$
(%i2) c4 : cycle_graph(4)$
(%i3) is_vertex_in_graph(0, c4);
(%o3)                         true
(%i4) is_vertex_in_graph(6, c4);
(%o4)                         false

Categories: Package graphs · Package graphs - properties

関数: is_tree (gr)

もし grが木なら trueを、そうでないなら falseを返します。

例:

(%i1) load (graphs)$
(%i2) is_tree(random_tree(4));
(%o2)                         true
(%i3) is_tree(graph_union(random_tree(4), random_tree(5)));
(%o3)                         false

Categories: Package graphs · Package graphs - properties

関数: laplacian_matrix (gr)

グラフ grの Laplace行列を返します。

例:

(%i1) load (graphs)$
(%i2) laplacian_matrix(cycle_graph(5));
                   [  2   - 1   0    0   - 1 ]
                   [                         ]
                   [ - 1   2   - 1   0    0  ]
                   [                         ]
(%o2)              [  0   - 1   2   - 1   0  ]
                   [                         ]
                   [  0    0   - 1   2   - 1 ]
                   [                         ]
                   [ - 1   0    0   - 1   2  ]

Categories: Package graphs · Package graphs - properties

関数: max_clique (gr)

グラフ grの最大クリークを返します。

例:

(%i1) load (graphs)$
(%i2) g : random_graph(100, 0.5)$
(%i3) max_clique(g);
(%o3)          [6, 12, 31, 36, 52, 59, 62, 63, 80]

Categories: Package graphs · Package graphs - properties

関数: max_degree (gr)

グラフ grの頂点の最大次数と最大次数の頂点を返します。

例:

(%i1) load (graphs)$
(%i2) g : random_graph(100, 0.02)$
(%i3) max_degree(g);
(%o3)                        [6, 79]
(%i4) vertex_degree(95, g);
(%o4)                           2

Categories: Package graphs · Package graphs - properties

関数: max_flow (net, s, t)

ソース sとシンク tを持ちネットワーク netを通る最大フローを返します。

関数は最大フローの値と最適フローで弧の重みを表現するリストを返します。

例:

(%i1) load (graphs)$
(%i2) net : create_graph(
  [1,2,3,4,5,6],
  [[[1,2], 1.0],
   [[1,3], 0.3],
   [[2,4], 0.2],
   [[2,5], 0.3],
   [[3,4], 0.1],
   [[3,5], 0.1],
   [[4,6], 1.0],
   [[5,6], 1.0]],
  directed=true)$
(%i3) [flow_value, flow] : max_flow(net, 1, 6);
(%o3) [0.7, [[[1, 2], 0.5], [[1, 3], 0.2], [[2, 4], 0.2],
[[2, 5], 0.3], [[3, 4], 0.1], [[3, 5], 0.1], [[4, 6], 0.3],
[[5, 6], 0.4]]]
(%i4) fl : 0$
(%i5) for u in out_neighbors(1, net)
     do fl : fl + assoc([1, u], flow)$
(%i6) fl;
(%o6)                          0.7

Categories: Package graphs · Package graphs - properties

関数: max_independent_set (gr)

グラフ grの最大独立集合を返します。

例:

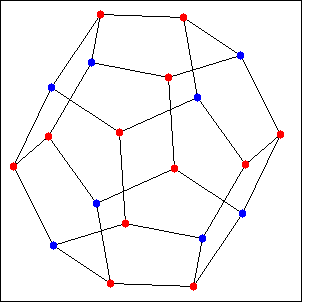
(%i1) load (graphs)$
(%i2) d : dodecahedron_graph()$
(%i3) mi : max_independent_set(d);
(%o3)             [0, 3, 5, 9, 10, 11, 18, 19]
(%i4) draw_graph(d, show_vertices=mi)$

Categories: Package graphs · Package graphs - properties

figures/graphs05

関数: max_matching (gr)

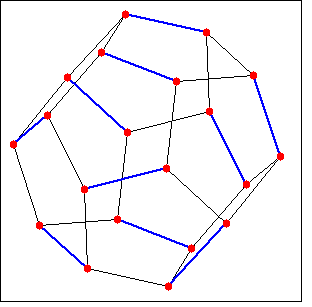
グラフ grの最大マッチングを返します。

例:

(%i1) load (graphs)$
(%i2) d : dodecahedron_graph()$
(%i3) m : max_matching(d);
(%o3) [[5, 7], [8, 9], [6, 10], [14, 19], [13, 18], [12, 17],
                               [11, 16], [0, 15], [3, 4], [1, 2]]
(%i4) draw_graph(d, show_edges=m)$

Categories: Package graphs · Package graphs - properties

figures/graphs06

関数: min_degree (gr)

グラフ grの頂点の最小次数と最小次数の頂点を返します。

例:

(%i1) load (graphs)$
(%i2) g : random_graph(100, 0.1)$
(%i3) min_degree(g);
(%o3)                        [3, 49]
(%i4) vertex_degree(21, g);
(%o4)                           9

Categories: Package graphs · Package graphs - properties

関数: min_edge_cut (gr)

グラフ grの最小切断辺を返します。

edge_connectivityも参照してください。

Categories: Package graphs · Package graphs - properties

関数: min_vertex_cover (gr)

グラフ grの最小頂点被覆を返します。

Categories: Package graphs · Package graphs - properties

関数: min_vertex_cut (gr)

グラフ grの最小頂点切断を返します。

vertex_connectivityも参照してください。

Categories: Package graphs · Package graphs - properties

関数: minimum_spanning_tree (gr)

グラフ grの最小全域木を返します。

例:

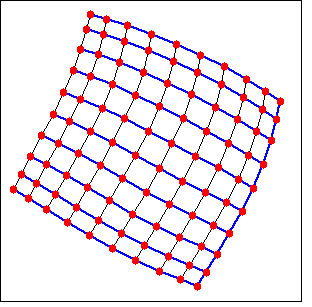
(%i1) load (graphs)$
(%i2) g : graph_product(path_graph(10), path_graph(10))$
(%i3) t : minimum_spanning_tree(g)$
(%i4) draw_graph(g, show_edges=edges(t))$

Categories: Package graphs · Package graphs - properties

figures/graphs07

関数: neighbors (v, gr)

グラフ grの頂点 vの隣接点のリストを返します。

例:

(%i1) load (graphs)$
(%i2) p : petersen_graph()$
(%i3) neighbors(3, p);
(%o3)                       [4, 8, 2]

Categories: Package graphs · Package graphs - properties

関数: odd_girth (gr)

グラフ grの最短奇閉路の長さを返します。

例:

(%i1) load (graphs)$
(%i2) g : graph_product(cycle_graph(4), cycle_graph(7))$
(%i3) girth(g);
(%o3)                           4
(%i4) odd_girth(g);
(%o4)                           7

Categories: Package graphs · Package graphs - properties

関数: out_neighbors (v, gr)

ダイグラフ grの頂点 vの外隣接点のリストを返します。

例:

(%i1) load (graphs)$
(%i2) p : path_digraph(3)$
(%i3) in_neighbors(2, p);
(%o3)                          [1]
(%i4) out_neighbors(2, p);
(%o4)                          []

Categories: Package graphs · Package graphs - properties

関数: planar_embedding (gr)

grの平面埋め込みでのfacial walkのリストを返します。もし grが平面グラフでないなら falseを返します。

グラフ grは二連結でなければいけません。

使われるアルゴリズムは Demoucronのアルゴリズムです。これは二次時間アルゴリズムです。

例:

(%i1) load (graphs)$
(%i2) planar_embedding(grid_graph(3,3));
(%o2) [[3, 6, 7, 8, 5, 2, 1, 0], [4, 3, 0, 1], [3, 4, 7, 6],
                                      [8, 7, 4, 5], [1, 2, 5, 4]]

Categories: Package graphs · Package graphs - properties

関数: print_graph (gr)

グラフ grについてのある情報を印字します。

例:

(%i1) load (graphs)$
(%i2) c5 : cycle_graph(5)$
(%i3) print_graph(c5)$
Graph on 5 vertices with 5 edges.
Adjacencies:
  4 :  0  3
  3 :  4  2
  2 :  3  1
  1 :  2  0
  0 :  4  1
(%i4) dc5 : cycle_digraph(5)$
(%i5) print_graph(dc5)$
Digraph on 5 vertices with 5 arcs.
Adjacencies:
  4 :  0
  3 :  4
  2 :  3
  1 :  2
  0 :  1
(%i6) out_neighbors(0, dc5);
(%o6)                          [1]

Categories: Package graphs

関数: radius (gr)

グラフ grの半径を返します。

例:

(%i1) load (graphs)$
(%i2) radius(dodecahedron_graph());
(%o2)                           5

Categories: Package graphs · Package graphs - properties

関数: set_edge_weight (e, w, gr)

グラフ grの辺 eに重み wを割り当てます。

例:

(%i1) load (graphs)$
(%i2) g : create_graph([1, 2], [[[1,2], 1.2]])$
(%i3) get_edge_weight([1,2], g);
(%o3)                          1.2
(%i4) set_edge_weight([1,2], 2.1, g);
(%o4)                         done
(%i5) get_edge_weight([1,2], g);
(%o5)                          2.1

Categories: Package graphs · Package graphs - properties

関数: set_vertex_label (v, l, gr)

グラフ grの頂点 vにラベル lを割り当てます。

例:

(%i1) load (graphs)$
(%i2) g : create_graph([[1, "One"], [2, "Two"]], [[1,2]])$
(%i3) get_vertex_label(1, g);
(%o3)                          One
(%i4) set_vertex_label(1, "oNE", g);
(%o4)                         done
(%i5) get_vertex_label(1, g);
(%o5)                          oNE

Categories: Package graphs · Package graphs - properties

関数: shortest_path (u, v, gr)

グラフ grの uから vまでの最短経路を返します。

例:

(%i1) load (graphs)$
(%i2) d : dodecahedron_graph()$
(%i3) path : shortest_path(0, 7, d);
(%o3)                   [0, 1, 19, 13, 7]
(%i4) draw_graph(d, show_edges=vertices_to_path(path))$

Categories: Package graphs · Package graphs - properties

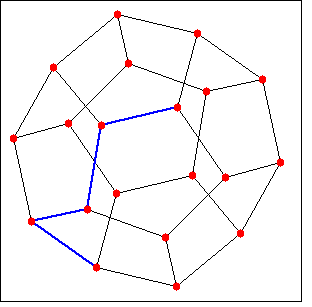
figures/graphs08

関数: shortest_weighted_path (u, v, gr)

グラフ grの uから vまでの最短重み付き経路とその長さを返します。

重み付き経路の長さは経路内の辺の辺重みの和です。もし辺に重みがないなら、辺はデフォルト重み1を持ちます。

例:

(%i1) load (graphs)$
(%i2) g: petersen_graph(20, 2)$
(%i3) for e in edges(g) do set_edge_weight(e, random(1.0), g)$
(%i4) shortest_weighted_path(0, 10, g);
(%o4) [2.575143920268482, [0, 20, 38, 36, 34, 32, 30, 10]]

Categories: Package graphs · Package graphs - properties

関数: strong_components (gr)

ダイグラフ grの強成分を返します。

例:

(%i1) load (graphs)$
(%i2) t : random_tournament(4)$
(%i3) strong_components(t);
(%o3)                 [[1], [0], [2], [3]]
(%i4) vertex_out_degree(3, t);
(%o4)                           3

Categories: Package graphs · Package graphs - properties

関数: topological_sort (dag)

Returns a topological sorting of the vertices of a directed graph ダイグラフ dagの頂点のトポロジカルソートを返します。もし dagが有向無閉路グラフなら空のリストを返します。

例:

(%i1) load (graphs)$
(%i2) g:create_graph(
         [1,2,3,4,5],
         [
          [1,2], [2,5], [5,3],
          [5,4], [3,4], [1,3]
         ],
         directed=true)$
(%i3) topological_sort(g);
(%o3)                    [1, 2, 5, 3, 4]

Categories: Package graphs · Package graphs - properties

関数: vertex_connectivity (g)

グラフ gの頂点連結性を返します。

min_vertex_cutも参照してください。

Categories: Package graphs · Package graphs - properties

関数: vertex_degree (v, gr)

グラフ grの頂点 vの次数を返します。

Categories: Package graphs · Package graphs - properties

関数: vertex_distance (u, v, gr)

(有向)グラフ grの uと vの間の最短経路の長さを返します。

例:

(%i1) load (graphs)$
(%i2) d : dodecahedron_graph()$
(%i3) vertex_distance(0, 7, d);
(%o3)                           4
(%i4) shortest_path(0, 7, d);
(%o4)                   [0, 1, 19, 13, 7]

Categories: Package graphs · Package graphs - properties

関数: vertex_eccentricity (v, gr)

グラフ grの頂点 vの離心率を返します。

例:

(%i1) load (graphs)$
(%i2) g:cycle_graph(7)$
(%i3) vertex_eccentricity(0, g);
(%o3)                           3

Categories: Package graphs · Package graphs - properties

関数: vertex_in_degree (v, gr)

ダイグラフ grの頂点 vの内次数を返します。

例:

(%i1) load (graphs)$
(%i2) p5 : path_digraph(5)$
(%i3) print_graph(p5)$
Digraph on 5 vertices with 4 arcs.
Adjacencies:
  4 :
  3 :  4
  2 :  3
  1 :  2
  0 :  1
(%i4) vertex_in_degree(4, p5);
(%o4)                           1
(%i5) in_neighbors(4, p5);
(%o5)                          [3]

Categories: Package graphs · Package graphs - properties

関数: vertex_out_degree (v, gr)

ダイグラフ grの頂点 vの外次数を返します。

例:

(%i1) load (graphs)$
(%i2) t : random_tournament(10)$
(%i3) vertex_out_degree(0, t);
(%o3)                           2
(%i4) out_neighbors(0, t);
(%o4)                        [7, 1]

Categories: Package graphs · Package graphs - properties

関数: vertices (gr)

グラフ grの頂点のリストを返します。

例:

(%i1) load (graphs)$
(%i2) vertices(complete_graph(4));
(%o2)                     [3, 2, 1, 0]

Categories: Package graphs · Package graphs - properties

関数: vertex_coloring (gr)

グラフ grの頂点の最適色付けを返します。

関数は、彩色数と grの頂点の色付けを表すリストを返します。

例:

(%i1) load (graphs)$
(%i2) p:petersen_graph()$
(%i3) vertex_coloring(p);
(%o3) [3, [[0, 2], [1, 3], [2, 2], [3, 3], [4, 1], [5, 3],
                                 [6, 1], [7, 1], [8, 2], [9, 2]]]

Categories: Package graphs · Package graphs - properties

関数: wiener_index (gr)

グラフ grのWiener指数を返します。

例:

(%i2) wiener_index(dodecahedron_graph());
(%o2)                          500

Categories: Package graphs · Package graphs - properties

[ < ]

[ > ]

[ << ]

[ Up ]

[ >> ]

[Top]

[Contents]

[Index]

[ ? ]

61.2.3 Modifying graphs

関数: add_edge (e, gr)

辺 eをグラフ grに加えます。

例:

(%i1) load (graphs)$
(%i2) p : path_graph(4)$
(%i3) neighbors(0, p);
(%o3)                          [1]
(%i4) add_edge([0,3], p);
(%o4)                         done
(%i5) neighbors(0, p);
(%o5)                        [3, 1]

Categories: Package graphs · Package graphs - modifications

関数: add_edges (e_list, gr)

リスト e_listの中の辺すべてをグラフ grに加えます。

例:

(%i1) load (graphs)$
(%i2) g : empty_graph(3)$
(%i3) add_edges([[0,1],[1,2]], g)$
(%i4) print_graph(g)$
Graph on 3 vertices with 2 edges.
Adjacencies:
  2 :  1
  1 :  2  0
  0 :  1

Categories: Package graphs · Package graphs - modifications

関数: add_vertex (v, gr)

頂点 vをグラフ grに加えます。

例:

(%i1) load (graphs)$
(%i2) g : path_graph(2)$
(%i3) add_vertex(2, g)$
(%i4) print_graph(g)$
Graph on 3 vertices with 1 edges.
Adjacencies:
  2 :
  1 :  0
  0 :  1

Categories: Package graphs · Package graphs - modifications

関数: add_vertices (v_list, gr)

リスト v_listの中の頂点すべてをグラフ grに加えます。

Categories: Package graphs · Package graphs - modifications

関数: connect_vertices (v_list, u_list, gr)

グラフ grに関して、リスト v_list内の頂点すべてをリスト u_list内の頂点に連結します。

v_listと u_listは1つの頂点か、頂点のリストを取り得ます。

例:

(%i1) load (graphs)$
(%i2) g : empty_graph(4)$
(%i3) connect_vertices(0, [1,2,3], g)$
(%i4) print_graph(g)$
Graph on 4 vertices with 3 edges.
Adjacencies:
  3 :  0
  2 :  0
  1 :  0
  0 :  3  2  1

Categories: Package graphs · Package graphs - modifications

関数: contract_edge (e, gr)

グラフ grの辺 eを縮約します。

例:

(%i1) load (graphs)$
(%i2) g: create_graph(
      8, [[0,3],[1,3],[2,3],[3,4],[4,5],[4,6],[4,7]])$
(%i3) print_graph(g)$
Graph on 8 vertices with 7 edges.
Adjacencies:
  7 :  4
  6 :  4
  5 :  4
  4 :  7  6  5  3
  3 :  4  2  1  0
  2 :  3
  1 :  3
  0 :  3
(%i4) contract_edge([3,4], g)$
(%i5) print_graph(g)$
Graph on 7 vertices with 6 edges.
Adjacencies:
  7 :  3
  6 :  3
  5 :  3
  3 :  5  6  7  2  1  0
  2 :  3
  1 :  3
  0 :  3

Categories: Package graphs · Package graphs - modifications

関数: remove_edge (e, gr)

グラフ grから辺 eを削除します。

例:

(%i1) load (graphs)$
(%i2) c3 : cycle_graph(3)$
(%i3) remove_edge([0,1], c3)$
(%i4) print_graph(c3)$
Graph on 3 vertices with 2 edges.
Adjacencies:
  2 :  0  1
  1 :  2
  0 :  2

Categories: Package graphs · Package graphs - modifications

関数: remove_vertex (v, gr)

グラフ grから頂点 vを削除します。

Categories: Package graphs

[ < ]

[ > ]

[ << ]

[ Up ]

[ >> ]

[Top]

[Contents]

[Index]

[ ? ]

61.2.4 Reading and writing to files

関数: dimacs_export
dimacs_export (gr, fl)
dimacs_export (gr, fl, comment1, ..., commentn)

グラフをファイル flにDIMACSフォーマットでエクスポートします。オプションのコメントはファイルの頭に加えられます。

Categories: Package graphs · Package graphs - io

関数: dimacs_import (fl)

DIMACSフォーマットのファイル flからグラフを返します。

Categories: Package graphs · Package graphs - io

関数: graph6_decode (str)

文字列 strに graph6フォーマットで符号化されたグラフを返します。

Categories: Package graphs · Package graphs - io

関数: graph6_encode (gr)

グラフ grを graph6フォーマットに符号化した文字列を返します。

Categories: Package graphs · Package graphs - io

関数: graph6_export (gr_list, fl)

リスト gr_list内のグラフをファイル flに graph6フォーマットでエクスポートします。

Categories: Package graphs · Package graphs - io

関数: graph6_import (fl)

graph6フォーマットのファイル flからグラフのリストを返します。

Categories: Package graphs · Package graphs - io

関数: sparse6_decode (str)

文字列 strに sparse6フォーマットで符号化されたグラフを返します。

Categories: Package graphs · Package graphs - io

関数: sparse6_encode (gr)

グラフ grを sparse6フォーマットに符号化した文字列を返します。

Categories: Package graphs · Package graphs - io

関数: sparse6_export (gr_list, fl)

リスト gr_list内のグラフをファイル flに sparse6フォーマットでエクスポートします。

Categories: Package graphs · Package graphs - io

関数: sparse6_import (fl)

sparse6フォーマットのファイル flからグラフのリストを返します。

Categories: Package graphs · Package graphs - io

[ < ]

[ > ]

[ << ]

[ Up ]

[ >> ]

[Top]

[Contents]

[Index]

[ ? ]

61.2.5 Visualization

関数: draw_graph
draw_graph (graph)
draw_graph (graph, option1, ..., optionk)

drawパッケージを使ってグラフを描画します。

頂点を配置するのに使われるアルゴリズムはオプション引数 programで指定されます。デフォルト値は program=spring_embeddingです。 draw_graphは頂点を配置するのに graphvizプログラムも使うことができますが、 graphvizを別途インストールしなければいけません。

例 1:

(%i1) load (graphs)$
(%i2) g:grid_graph(10,10)$
(%i3) m:max_matching(g)$
(%i4) draw_graph(g,
   spring_embedding_depth=100,
   show_edges=m, edge_type=dots,
   vertex_size=0)$

figures/graphs09

例 2:

(%i1) load (graphs)$
(%i2) g:create_graph(16,
    [
     [0,1],[1,3],[2,3],[0,2],[3,4],[2,4],
     [5,6],[6,4],[4,7],[6,7],[7,8],[7,10],[7,11],
     [8,10],[11,10],[8,9],[11,12],[9,15],[12,13],
     [10,14],[15,14],[13,14]
    ])$
(%i3) t:minimum_spanning_tree(g)$
(%i4) draw_graph(
    g,
    show_edges=edges(t),
    show_edge_width=4,
    show_edge_color=green,
    vertex_type=filled_square,
    vertex_size=2
    )$

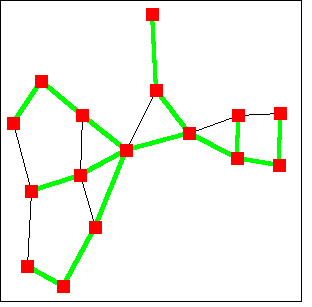
figures/graphs10

例 3:

(%i1) load (graphs)$
(%i2) g:create_graph(16,
    [
     [0,1],[1,3],[2,3],[0,2],[3,4],[2,4],
     [5,6],[6,4],[4,7],[6,7],[7,8],[7,10],[7,11],
     [8,10],[11,10],[8,9],[11,12],[9,15],[12,13],
     [10,14],[15,14],[13,14]
    ])$
(%i3) mi : max_independent_set(g)$
(%i4) draw_graph(
    g,
    show_vertices=mi,
    show_vertex_type=filled_up_triangle,
    show_vertex_size=2,
    edge_color=cyan,
    edge_width=3,
    show_id=true,
    text_color=brown
    )$

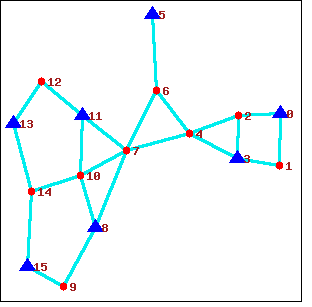
figures/graphs11

例 4:

(%i1) load (graphs)$
(%i2) net : create_graph(
    [0,1,2,3,4,5],
    [
     [[0,1], 3], [[0,2], 2],
     [[1,3], 1], [[1,4], 3],
     [[2,3], 2], [[2,4], 2],
     [[4,5], 2], [[3,5], 2]
    ],
    directed=true
    )$
(%i3) draw_graph(
    net,
    show_weight=true,
    vertex_size=0,
    show_vertices=[0,5],
    show_vertex_type=filled_square,
    head_length=0.2,
    head_angle=10,
    edge_color="dark-green",
    text_color=blue
    )$

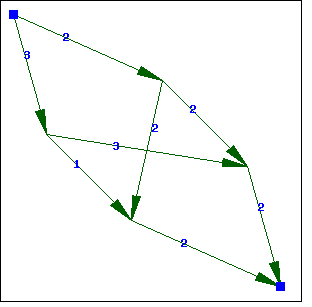
figures/graphs12

例 5:

(%i1) load(graphs)$
(%i2) g: petersen_graph(20, 2);
(%o2)                         GRAPH
(%i3) draw_graph(g, redraw=true, program=planar_embedding);
(%o3)                         done

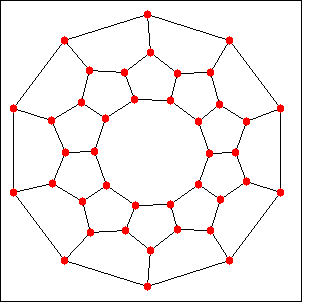
figures/graphs14

例 6:

(%i1) load(graphs)$
(%i2) t: tutte_graph();
(%o2)                         GRAPH
(%i3) draw_graph(t, redraw=true,
                    fixed_vertices=[1,2,3,4,5,6,7,8,9]);
(%o3)                         done

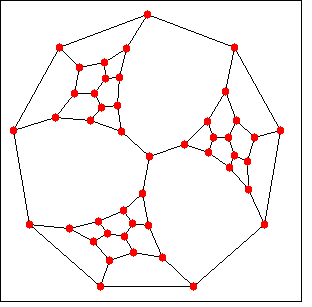
figures/graphs15

Categories: Package graphs

オプション変数: draw_graph_program

デフォルト値: spring_embedding

頂点を配置するのに使われるプログラムのデフォルト値は draw_graphプログラムです。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: show_id

デフォルト値: false

もし trueなら頂点の idが表示されます。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: show_label

デフォルト値: false

もし trueなら頂点のラベルが表示されます。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: label_alignment

デフォルト値: center

頂点のラベル/idをいかに整列させるか決めます。 left, center, rightであり得ます。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: show_weight

デフォルト値: false

もし trueなら辺の重みを表示します。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: vertex_type

デフォルト値: circle

頂点をいかに表示するか定義します。可能な値に関しては drawパッケージの point_typeオプションを参照してください。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: vertex_size

頂点のサイズ。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: vertex_color

頂点を表示するのに使う色。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: show_vertices

デフォルト値: []

選択された頂点を異なる色を使って表示。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: show_vertex_type

show_verticesで指定された頂点をいかに表示するか定義します。可能な値については drawパッケージの point_typeオプションを参照してください。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: show_vertex_size

show_vertices内の頂点のサイズ。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: show_vertex_color

show_verticesリスト内の頂点を表示するのに使う色。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: vertex_partition

デフォルト値: []

グラフの頂点の分割 [[v1,v2,...],...,[vk,...,vn]]分割内のそれぞれのリストの頂点を異なる色で描画します。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: vertex_coloring

頂点の色付けを指定します。色付け colは vertex_coloringが返すようなフォーマットで指定されなければいけません。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: edge_color

辺を表示するのに使われる色。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: edge_width

辺の幅。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: edge_type

辺をどう表示するか定義します。 drawパッケージの line_typeオプションを参照してください。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: show_edges

異なる色を使ってリスト e_list内で指定された辺を表示します。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: show_edge_color

show_edgesリスト内の辺を表示するのに使う色。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: show_edge_width

show_edges内の辺の幅。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: show_edge_type

show_edges内の辺を以下に表示するかを定義します。 drawパッケージの line_typeオプションを参照してください。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: edge_partition

グラフの辺の分割 [[e1,e2,...],...,[ek,...,em]]分割内のそれぞれのリストの辺を異なる色を使って描画します。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: edge_coloring

辺の色付け。色付けは関数 edge_coloringが返すようなフォーマットで指定しなければいけません。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: redraw

デフォルト値: false

もし trueなら、たとえ位置がグラフの以前の描画から保存されていても頂点位置を再計算します。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: head_angle

デフォルト値: 15

(ダイグラフの)弧に表示される矢印の角度。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: head_length

デフォルト値: 0.1

(ダイグラフの)弧に表示される矢印の長さ。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: spring_embedding_depth

デフォルト値: 50

バネ埋め込みグラフ描画アルゴリズムでの繰り返し回数。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: terminal

描画で使う端末。 (drawパッケージの terminalオプションを参照してください。)

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: file_name

端末がスクリーンでないなら描画のファイル名。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: program

グラフの頂点を配置するのに使われるプログラムを定義します。 graphvizプログラム (dot, neato, twopi, circ, fdp)の1つ, circular, spring_embedding, planar_embeddingを取り得ます。二連結平面グラフでは planar_embeddingだけが利用可能です。 program=spring_embeddingの時、固定位置の頂点の集合が fixed_verticesオプションで指定可能です。

Categories: Package graphs · Package graphs - draw_graphs options

draw_graphオプション: fixed_vertices

正多角形沿いに固定された位置を持つ頂点のリストを指定します。 program=spring_embeddingの時、使うことができます。

Categories: Package graphs · Package graphs - draw_graphs options

関数: vertices_to_path (v_list)

頂点のリスト v_listを v_listで定義された経路の辺のリストに変換します。

Categories: Package graphs

関数: vertices_to_cycle (v_list)

頂点のリスト v_listを v_listで定義された閉路の辺のリストに変換します。

Categories: Package graphs

[ << ]

[ >> ]

[Top]

[Contents]

[Index]

[ ? ]

This document was generated by 市川雄二 on June, 21 2016 using texi2html 1.76.