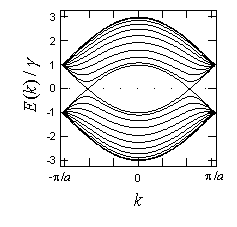
図1(a):強結合モデルによる(10,10)アームチェアナノチューブの分散関係.フェルミエネルギーを0とした.フェルミ面は2つの点からなり,その間の散乱は無視する.
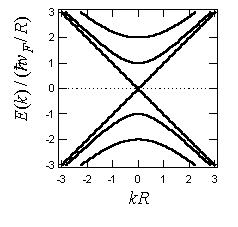
図1(b):有効質量方程式によるフェルミ点付近の分散関係.Rはチューブの半径.二つの線形分散を持つモード間の散乱のみを考慮する.
東京大学物性研究所 鈴浦秀勝,安藤恒也
金属カーボンナノチューブは理想的な1次元導体とみなせるが,通常の不純物ポテンシャルでは電子が散乱されないという特筆すべき性質を持っている[1,2].室温において多層ナノチューブの量子化コンダクタンスが観測されたという報告もあり[3],従来の量子細線と比較して非常に大きな電気伝導率を持つ物質として期待される.不純物の他に,特に高温において,主に電気抵抗に寄与するのは電子・格子散乱である.我々はフェルミ点近傍の電子系に対する有効質量方程式に基づいて電子・格子散乱を議論した.ただし,室温程度で励起される長波長の音響フォノンによる散乱のみを考慮し,2つのフェルミ点間の散乱,いわゆる谷間散乱,を無視した
(図1参照).
グラファイト平面の長波長音響フォノンモードは結晶の等方性を反映して等方的弾性体モデルにより記述される.カーボンナノチューブはグラファイト平面を丸めてつなげたものと考えることができるが,平面に単に周期的境界条件を課すだけでは表現できないことに注意が必要である[4].その典型的な例としてナノチューブにおけるブリージングモードの存在があげられる.このブリージングモードは周方向に一様な面外振動で(図2参照),平面の場合は面に垂直方向の平行移動でゼロエネルギーであった変位が,ナノチューブでは面内方向の伸縮が生じることから有限のエネルギーを持つ.このように低エネルギーの格子振動は本質的に系のトポロジーを反映していることから,電子・格子相互作用を介して輸送現象にもナノチューブのトポロジーの影響が現れる可能性が示唆される.我々は,最隣接炭素原子間を結ぶボンドの伸長と隣接する2つのボンドがなす角の変化に対する2つの相互作用定数をナノチューブに対して導入した格子モデルから出発し,長波長極限の摂導展開により,ナノチューブの対称性を保存した音響フォノンに対する有効連続体モデルを導出した.このモデルの固有モードを用いて電子・格子散乱確率を計算することにより,ナノチューブの電気抵抗の温度依存性を調べた.
フェルミ点近傍の電子の運動は質量ゼロのディラック方程式,いわゆるワイル方程式,で記述される[5].ハミルトニアンは1つのフェルミ点に着目すれば2行2列の行列になり,電子・格子相互作用も行列として導入される.まず,対角項として通常の変形ポテンシャルが存在する.格子変位ベクトルの発散に比例して,体積変化を伴う縦モードのみが相互作用に関与する.非対角項には格子変位による電子構造の変調を表わす相互作用項が存在する.この非対角項は,有効質量方程式の高次補正項と同様に,ナノチューブのカイラル角,つまり,螺旋度に依存している.相互作用定数の大きさはグラファイトで用いられるパラメータから,対角項が約20eV,非対角項が約8eVと見積もられ,グラファイトの場合は対角項の変形ポテンシャルが電気抵抗の主な起源と考えられている.
ナノチューブの場合,低エネルギーの長波長フォノンによる散乱を議論する限り,電子は線形分散を持つ2つの1次元的な固有モードを取り扱えば良い(図1(b)参照).電気抵抗は電子の後方散乱確率を計算することにより得られるが,この時,対角項の変形ポテンシャルは不純物ポテンシャルの場合と同じく散乱に全く寄与しないことがわかる.この事情は,グラファイト平面において180度の後方散乱確率がゼロであるという事実そのもので,ナノチューブにおいては運動が1次元的になり,180度からずれた散乱がありえないことから対角項が後方散乱に寄与しないということになっている.よって,ナノチューブはグラファイトより大きな電気伝導率を持つことが期待される.非対角項は有限の散乱を生じるが,その実部のみが散乱に寄与することが明らかになった.非対角項は螺旋度に依存することから,電気抵抗もまた螺旋度に依存する可能性がある.
さらに,フォノン散乱では運動量保存が成立することに着目する.電子の波動関数は円周方向に一様であるため,散乱に寄与する格子振動も円周方向に一様なモードに制限される.そのようなモードは,チューブの径が一様に伸縮するブリージング(B)モード,チューブが一様に伸縮するストレッチング(S)モード,チューブが軸の周りに一様にねじれるツイスト(T)モードの3種類が存在する(図2参照).連続体モデルで得られるこれらのモードの分散関係を図3に示す.ジグザグナノチューブではとBモード
Sモードが,アームチェアーナノチューブではTモードが,中間の螺旋度ではすべてのモードが散乱に寄与して,カイラル角が変化するにしたがってその比率が移り変わることが明らかになった.
高温極限において,フォノン散乱の確率は励起されているフォノンの数,つまり,温度に比例する.高温近似の適用範囲は後方散乱に必要な波数のフォノンのエネルギーで決まるが,ナノチューブのフェルミ点近傍における後方散乱では,通常の1次元金属でkFと-kFを結ぶような大きな運動量変化を伴わないため,フォノンの速度が電子の速度に比べて無視できるとすれば,室温より充分低温まで高温近似が成立する[6].そこで,すべてのフォノンモードに対して高温近似を適用して散乱確率を計算すると,カイラル角に依存しない結果が得られた.つまり,金属カーボンナノチューブの電気抵抗は温度に比例し,その比例係数は螺旋度に依存しない.
しかし,温度を下げていくと事情は異なる.SモードとTモードは長波長極限で線形分散を持ちゼロモードになるのに対して,Bモードはエネルギーギャップを持っている.よって,温度がBモードのエネルギーと同程度になるとBモードに対する高温近似は破綻する.ところが,チューブの伸縮と径の伸縮は有限の波数では分離することができず,実際,上でも述べたようにBモードと電子が相互作用する時は必ずSモードとも結合している.よって,Bモードの励起が少なくなってもSモードは充分に励起されており,Bモードによる散乱が減少するだけで,全体として高温近似は成立している.つまり,励起されたフォノンの数を,高温近似せず,ボーズ分布関数で表わせばBモードのエネルギー以下の低温まで計算が可能で,数値的に計算した電気抵抗の温度依存性を図4に示す.上で述べたように,高温極限では螺旋度に依らず温度に比例し,アームチェアでは低温まで一様に減少するが[6],その他の場合,Bモードのエネルギーに対応する温度付近で抵抗が減少しはじめ,更に低温では比例係数は小さくなるが温度に比例して減少する振る舞いが見られる.この抵抗の減少が一番顕著なのはBモードの寄与が最も大きいジグザグチューブで,低温でBモードの散乱の寄与がなくなるという定性的説明と合致する.
以上のように,金属カーボンナノチューブのフォノン散乱に起因する電気抵抗はアームチェアナノチューブでは温度に単純に比例して増加するのに対して,ジグザグ,カイラルチューブでは,散乱に寄与するブリージングモードが有限のエネルギーギャップを持つことにより低温では励起されず,抵抗が減少するという結果が得られた.つまり,金属カーボンナノチューブの輸送特性はカイラル角,すなわち,螺旋度に依存すると結論される.音響フォノン系と電子系がともに低エネルギーで螺旋度に依存しない有効モデルで記述されることを考えると,この事実は容易には想像できないかもしれない.しかし,高温極限では金属ナノチューブが1次元的な導線とみなせて,細かい構造が見えなくなってしまうという描像が正しく,ある程度,温度が下がって,単なる線ではないチューブという構造が見えてきたとき,螺旋度に依存した電子・格子相互作用を介してチューブの構造が輸送現象に現れるということから,ナノチューブの構造を特徴的に反映している現象であると言えるだろう.
この内容の一部はMolecular Crystals and
Liquid Crystals に10th INTERNATIONAL
SYMPOSIUM ON INTERCALATION COMPOUNDSの会議録の論文として掲載予定である.
[1] T. Ando and T. Nakanishi, J. Phys. Soc. Jpn. 67,
1704 (1998),
[2] T. Ando, T. Nakanishi, and R. Saito, J. Phys. Soc.
Jpn. 67, 2857 (1998).
[3] S. Frank et
al., Science 280, 1744 (1998).
[4] R. Saito, G. Dresselhaus, and M. S. Dresselhaus, Physical Properties of Carbon
Naonotubes (Imperial College Press, London, 1998).
[5] H. Ajiki and T. Ando, J. Phys. Soc. Jpn. 62, 1255 (1993).
[6] C. L. Kane et al.,
Europhys. Lett. 41, 683 (1998)

図1(a):強結合モデルによる(10,10)アームチェアナノチューブの分散関係.フェルミエネルギーを0とした.フェルミ面は2つの点からなり,その間の散乱は無視する.

図1(b):有効質量方程式によるフェルミ点付近の分散関係.Rはチューブの半径.二つの線形分散を持つモード間の散乱のみを考慮する.
変 ブリージング ストレッチング ツィスティング
![]()




図2: 振動モードに対する変形の模式図.
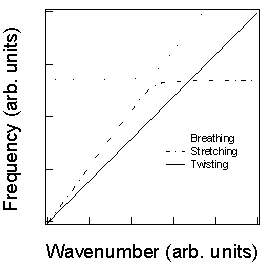
図3:フォノンモードの分散関係.ブリージングとストレッチングは波数ゼロ付近の振動の様子から名前をつけた.二つのエネルギーが接近するのは波数1/R近傍.
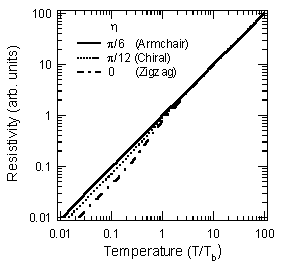
図4:カーボンナノチューブの電気抵抗の温度依存性.ただし, Tbはブリージングモードのエネルギーに対応する温度を表わす.